Clustering analysis is used to find groups of similar objects in a dataset. There are two main categories of clustering:
- Hierarchical clustering: like agglomerative (hclust and agnes) and divisive (diana) methods, which construct a hierarchy of clustering.
- Partitioning clustering: like k-means, pam, clara and fanny, which require the user to specify the number of clusters to be generated.
These clustering methods can be computed using the R packages stats (for k-means) and cluster (for pam, clara and fanny), but the workflow require multiple steps and multiple lines of R codes.
In this chapter, we provide some easy-to-use functions for enhancing the workflow of clustering analyses and we implemented ggplot2 method for visualizing the results.
1 Required package
The following R packages are required in this chapter:
- factoextra for enhanced clustering analyses and data visualization
- cluster for computing the standard PAM, CLARA, FANNY, AGNES and DIANA clustering
- factoextra can be installed as follow:
if(!require(devtools)) install.packages("devtools")
devtools::install_github("kassambara/factoextra")- Install cluster:
install.packages("cluster")- Load required packages:
library(factoextra)
library(cluster)2 Data preparation
The built-in R dataset USArrests is used:
# Load and scale the dataset
data("USArrests")
df <- scale(USArrests)
head(df)## Murder Assault UrbanPop Rape
## Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
## Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
## Arizona 0.07163341 1.4788032 0.9989801 1.042878388
## Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
## California 0.27826823 1.2628144 1.7589234 2.067820292
## Colorado 0.02571456 0.3988593 0.8608085 1.8649672073 Enhanced distance matrix computation and visualization
This section describes two functions:
- get_dist() [in factoextra]: for computing distance matrix between rows of a data matrix. Compared to the standard dist() function, it supports correlation-based distance measures including pearson, kendall and spearman methods.
- fviz_dist(): for visualizing a distance matrix
# Correlation-based distance method
res.dist <- get_dist(df, method = "pearson")
head(round(as.matrix(res.dist), 2))[, 1:6]## Alabama Alaska Arizona Arkansas California Colorado
## Alabama 0.00 0.71 1.45 0.09 1.87 1.69
## Alaska 0.71 0.00 0.83 0.37 0.81 0.52
## Arizona 1.45 0.83 0.00 1.18 0.29 0.60
## Arkansas 0.09 0.37 1.18 0.00 1.59 1.37
## California 1.87 0.81 0.29 1.59 0.00 0.11
## Colorado 1.69 0.52 0.60 1.37 0.11 0.00# Visualize the dissimilarity matrix
fviz_dist(res.dist, lab_size = 8)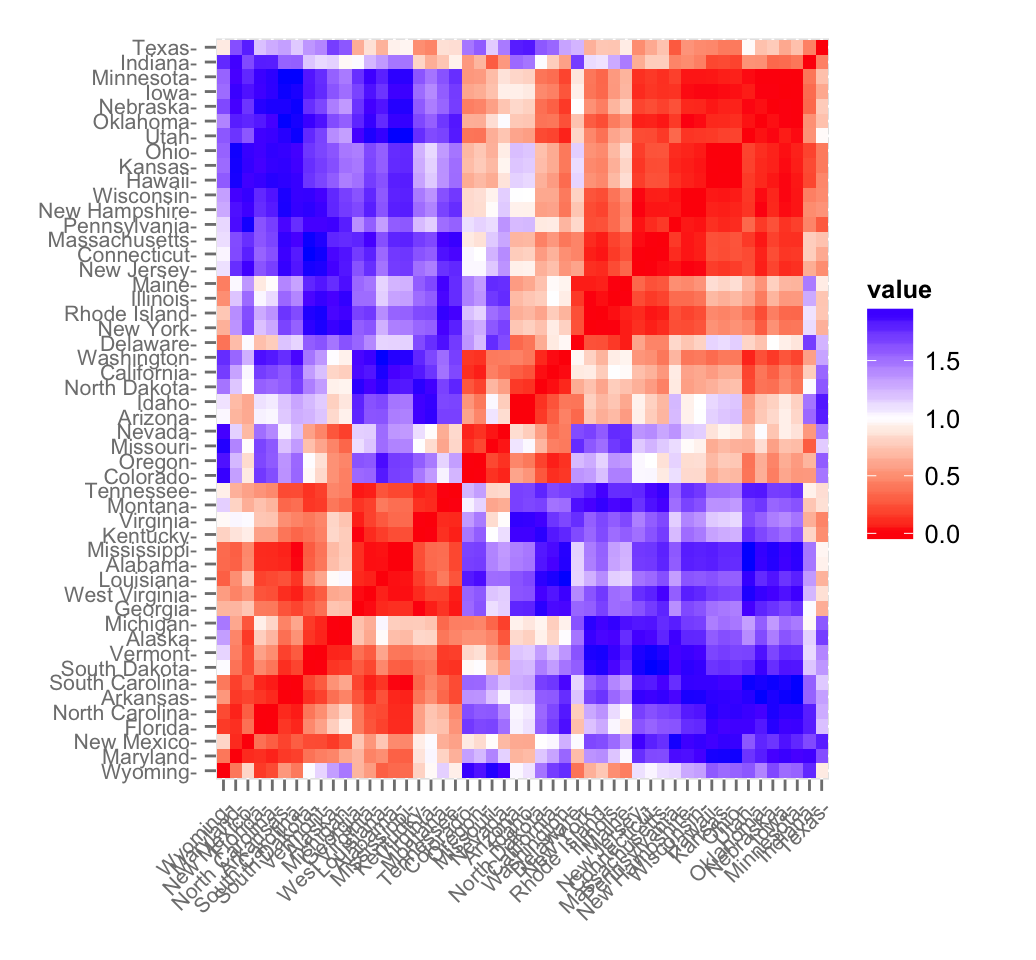
The ordered dissimilarity matrix image (ODI) displays the clustering tendency of the dataset. Similar objects are close to one another. Red color corresponds to small distance and blue color indicates big distance between observation.
4 Enhanced clustering analysis
For instance, the standard R code for computing hierarchical clustering is as follow:
# Load and scale the dataset
data("USArrests")
df <- scale(USArrests)
# Compute dissimilarity matrix
res.dist <- dist(df, method = "euclidean")
# Compute hierarchical clustering
res.hc <- hclust(res.dist, method = "ward.D2")
# Visualize
plot(res.hc, cex = 0.5)
In this chapter, we provide the function eclust() [in factoextra] which provides several advantages:
- It simplifies the workflow of clustering analysis
- It can be used to compute hierarchical clustering and partititioning clustering in a single line function call
- Compared to the standard partitioning functions (kmeans, pam, clara and fanny) which requires the user to specify the optimal number of clusters, the function eclust() computes automatically the gap statistic for estimating the right number of clusters.
- For hierarchical clustering, correlation-based metric is allowed
- It provides silhouette information for all partitioning methods and hierarchical clustering
- It draws beautiful graphs using ggplot2
4.1 eclust() function
eclust(x, FUNcluster = "kmeans", hc_metric = "euclidean", ...)- x: numeric vector, data matrix or data frame
- FUNcluster: a clustering function including kmeans, pam, clara, fanny, hclust, agnes and diana. Abbreviation is allowed.
- hc_metric: character string specifying the metric to be used for calculating dissimilarities between observations. Allowed values are those accepted by the function dist() [including euclidean, manhattan, maximum, canberra, binary, minkowski] and correlation based distance measures [pearson, spearman or kendall]. Used only when FUNcluster is a hierarchical clustering function such as one of hclust, agnes or diana.
- : other arguments to be passed to FUNcluster.
The function eclust() returns an object of class eclust containing the result of the standard function used (e.g., kmeans, pam, hclust, agnes, diana, etc.).
It includes also:
- cluster: the cluster assignment of observations after cutting the tree
- nbclust: the number of clusters
- silinfo: the silhouette information of observations
- size: the size of clusters
- data: a matrix containing the original or the standardized data (if stand = TRUE)
- gap_stat: containing gap statistics
4.2 Examples
In this section well show some examples for enhanced k-means clustering and hierarchical clustering. Note that the same analysis can be done for PAM, CLARA, FANNY, AGNES and DIANA.
library("factoextra")
# Enhanced k-means clustering
res.km <- eclust(df, "kmeans", nstart = 25)
# Gap statistic plot
fviz_gap_stat(res.km$gap_stat)
# Silhouette plot
fviz_silhouette(res.km)## cluster size ave.sil.width
## 1 1 8 0.39
## 2 2 16 0.34
## 3 3 13 0.37
## 4 4 13 0.27
# Optimal number of clusters using gap statistics
res.km$nbclust## [1] 4# Print result
res.km## K-means clustering with 4 clusters of sizes 8, 16, 13, 13
##
## Cluster means:
## Murder Assault UrbanPop Rape
## 1 1.4118898 0.8743346 -0.8145211 0.01927104
## 2 -0.4894375 -0.3826001 0.5758298 -0.26165379
## 3 -0.9615407 -1.1066010 -0.9301069 -0.96676331
## 4 0.6950701 1.0394414 0.7226370 1.27693964
##
## Clustering vector:
## Alabama Alaska Arizona Arkansas California
## 1 4 4 1 4
## Colorado Connecticut Delaware Florida Georgia
## 4 2 2 4 1
## Hawaii Idaho Illinois Indiana Iowa
## 2 3 4 2 3
## Kansas Kentucky Louisiana Maine Maryland
## 2 3 1 3 4
## Massachusetts Michigan Minnesota Mississippi Missouri
## 2 4 3 1 4
## Montana Nebraska Nevada New Hampshire New Jersey
## 3 3 4 3 2
## New Mexico New York North Carolina North Dakota Ohio
## 4 4 1 3 2
## Oklahoma Oregon Pennsylvania Rhode Island South Carolina
## 2 2 2 2 1
## South Dakota Tennessee Texas Utah Vermont
## 3 1 4 2 3
## Virginia Washington West Virginia Wisconsin Wyoming
## 2 2 3 3 2
##
## Within cluster sum of squares by cluster:
## [1] 8.316061 16.212213 11.952463 19.922437
## (between_SS / total_SS = 71.2 %)
##
## Available components:
##
## [1] "cluster" "centers" "totss" "withinss"
## [5] "tot.withinss" "betweenss" "size" "iter"
## [9] "ifault" "clust_plot" "silinfo" "nbclust"
## [13] "data" "gap_stat" # Enhanced hierarchical clustering
res.hc <- eclust(df, "hclust") # compute hclust
fviz_dend(res.hc, rect = TRUE) # dendrogam
fviz_silhouette(res.hc) # silhouette plot## cluster size ave.sil.width
## 1 1 7 0.40
## 2 2 12 0.26
## 3 3 18 0.38
## 4 4 13 0.35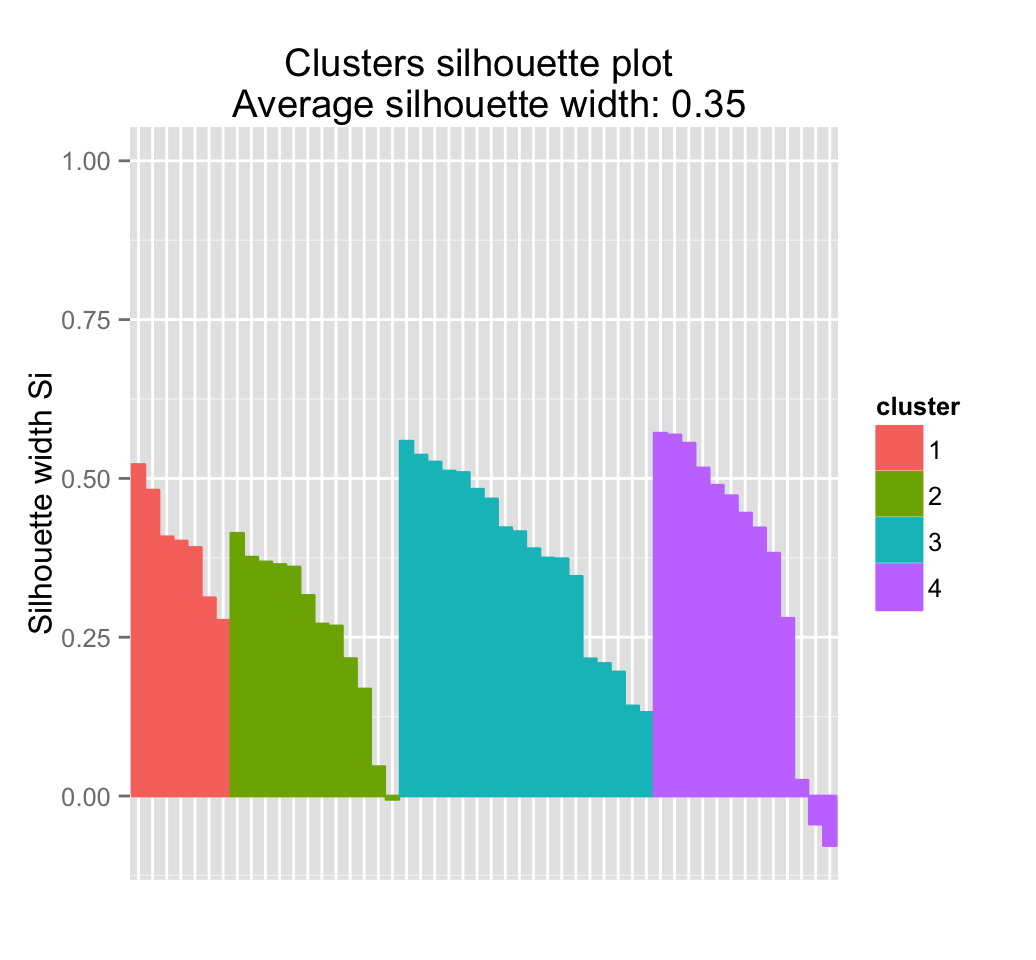
fviz_cluster(res.hc) # scatter plot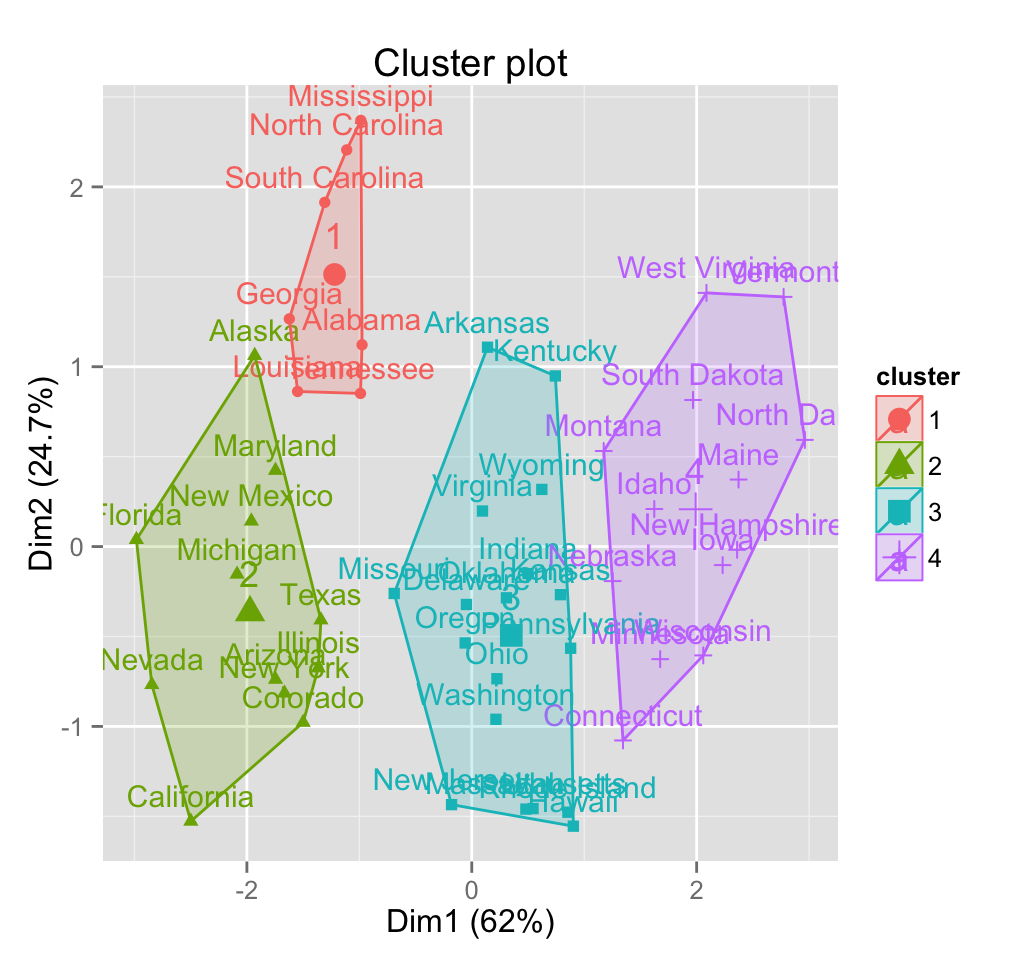
Its also possible to specify the number of clusters as follow:
eclust(df, "kmeans", k = 4)5 Infos
This analysis has been performed using R software (ver. 3.2.1)