- Required packages
- Load FactoMineR and factoextra
- Data format
- Exploratory data analysis
- Multiple Correspondence Analysis (MCA)
- Summary of MCA outputs
- Interpretation of MCA outputs
- Eigenvalues/variances and screeplot
- MCA scatter plot: Biplot of individuals and variable categories
- Variable categories
- Individuals
- MCA using supplementary individuals and variables
- Filter the MCA result
- Dimension description
- Infos
- References and further reading
As described in my previous article, the simple correspondence analysis (CA) is used to analyse the contingency table formed by two categorical variables.
To learn more about CA, read this article: Correspondence Analysis in R: The Ultimate Guide for the Analysis, the Visualization and the Interpretation.
Multiple Correspondence Analysis (MCA) is an extension of simple CA to analyse a data table containing more than two categorical variables.
MCA is generally used to analyse a data from survey.
The objectives are to identify:
- A group of individuals with similar profile in their answers to the questions
- The associations between variable categories
There are several R functions from different packages to compute MCA, including:
- MCA() [in FactoMineR package]
- dudi.mca() [in ade4 package]
These packages provide also some standard functions to visualize the results of the analysis. Its also possible to use the package factoextra to generate easily beautiful graphs.
This article describes how to perform and interpret multiple correspondence analysis using FactoMineR package.
Required packages
FactoMineR(for computing MCA) and factoextra (for MCA visualization) packages are used.
These packages can be installed as follow :
install.packages("FactoMineR")
# install.packages("devtools")
devtools::install_github("kassambara/factoextra")Note that, for factoextra a version >= 1.0.2 is required for this tutorial. If its already installed on your computer, you should re-install it to have the most updated version.
Load FactoMineR and factoextra
library("FactoMineR")
library("factoextra")Data format
Well use the data sets poison [in FactoMineR]
data(poison)
head(poison[, 1:7]) Age Time Sick Sex Nausea Vomiting Abdominals
1 9 22 Sick_y F Nausea_y Vomit_n Abdo_y
2 5 0 Sick_n F Nausea_n Vomit_n Abdo_n
3 6 16 Sick_y F Nausea_n Vomit_y Abdo_y
4 9 0 Sick_n F Nausea_n Vomit_n Abdo_n
5 7 14 Sick_y M Nausea_n Vomit_y Abdo_y
6 72 9 Sick_y M Nausea_n Vomit_n Abdo_yAn image of the data is shown below:
This data is a result from a survey carried out on children of primary school who suffered from food poisoning. They were asked about their symptoms and about what they ate.
The data contains 55 rows (children, individuals) and 15 columns (variables).
Only some of these individuals (children) and variables will be used to perform the multiple correspondence analysis (MCA).
The coordinates of the remaining individuals and variables on the factor map will be predicted after the MCA.In MCA terminology, our data contains :
- Active individuals (rows 1:55): Individuals that are used during the correspondence analysis.
- Active variables (columns 5:15) : Variables that are used for the MCA.
- Supplementary variables : They dont participate to the MCA. The coordinates of these variables will be predicted.
- Supplementary continuous variables : Columns 1 and 2 corresponding to the columns age and time, respectively.
- Supplementary qualitative variables : Columns 3 and 4 corresponding to the columns Sick and Sex, respectively. This factor variables will be used to color individuals by groups.
Subset only active individuals and variables for multiple correspondence analysis:
poison.active <- poison[1:55, 5:15]
head(poison.active[, 1:6]) Nausea Vomiting Abdominals Fever Diarrhae Potato
1 Nausea_y Vomit_n Abdo_y Fever_y Diarrhea_y Potato_y
2 Nausea_n Vomit_n Abdo_n Fever_n Diarrhea_n Potato_y
3 Nausea_n Vomit_y Abdo_y Fever_y Diarrhea_y Potato_y
4 Nausea_n Vomit_n Abdo_n Fever_n Diarrhea_n Potato_y
5 Nausea_n Vomit_y Abdo_y Fever_y Diarrhea_y Potato_y
6 Nausea_n Vomit_n Abdo_y Fever_y Diarrhea_y Potato_yExploratory data analysis
The function summary() can be used to compute the frequency of variable categories. As the data table contains a large number of variables, well display only the results for the first 4 variables.
Statistical summaries:
# Summary of the 4 first variables
summary(poison.active)[, 1:4] Nausea Vomiting Abdominals Fever "Nausea_n:43 " "Vomit_n:33 " "Abdo_n:18 " "Fever_n:20 ""Nausea_y:12 " "Vomit_y:22 " "Abdo_y:37 " "Fever_y:35 "Its also possible to plot the frequency of variable categories:
for (i in 1:ncol(poison.active)) {
plot(poison.active[,i], main=colnames(poison.active)[i],
ylab = "Count", col="steelblue", las = 2)
}










The graphs above can be used to identify variable categories with a very low frequency. These types of variables can distort the analysis.
Multiple Correspondence Analysis (MCA)
The function MCA() [in FactoMineR package] can be used. A simplified format is :
MCA(X, ncp = 5, graph = TRUE)- X : a data frame with n rows (individuals) and p columns (categorical variables)
- ncp : number of dimensions kept in the final results.
- graph : a logical value. If TRUE a graph is displayed.
In the R code below, the MCA is performed only on the active individuals/variables :
res.mca <- MCA(poison.active, graph = FALSE)The output of the function MCA() is a list including :
print(res.mca)**Results of the Multiple Correspondence Analysis (MCA)**
The analysis was performed on 55 individuals, described by 11 variables
*The results are available in the following objects:
name description
1 "$eig" "eigenvalues"
2 "$var" "results for the variables"
3 "$var$coord" "coord. of the categories"
4 "$var$cos2" "cos2 for the categories"
5 "$var$contrib" "contributions of the categories"
6 "$var$v.test" "v-test for the categories"
7 "$ind" "results for the individuals"
8 "$ind$coord" "coord. for the individuals"
9 "$ind$cos2" "cos2 for the individuals"
10 "$ind$contrib" "contributions of the individuals"
11 "$call" "intermediate results"
12 "$call$marge.col" "weights of columns"
13 "$call$marge.li" "weights of rows" The object that is created using the function MCA() contains results as lists. These values are described in the next sections.
Summary of MCA outputs
The function summary.MCA() [in FactoMineR] is used to print a summary of multiple correspondence analysis results:
summary(object, nb.dec = 3, nbelements = 10,
ncp = TRUE, file ="", ...)- object: an object of class MCA
- nb.dec: number of decimal printed
- nbelements: number of row/column variables to be written. To have all the elements, use nbelements = Inf.
- ncp: Number of dimensions to be printed
- file: an optional file name for exporting the summaries.
Print the summary of the MCA for the dimensions 1 and 2:
summary(res.mca, nb.dec = 2, ncp = 2)
Eigenvalues
Dim.1 Dim.2 Dim.3 Dim.4 Dim.5 Dim.6 Dim.7 Dim.8 Dim.9 Dim.10 Dim.11
Variance 0.34 0.13 0.11 0.10 0.08 0.07 0.06 0.06 0.04 0.01 0.01
% of var. 33.52 12.91 10.73 9.59 7.88 7.11 6.02 5.58 4.12 1.30 1.23
Cumulative % of var. 33.52 46.44 57.17 66.76 74.64 81.75 87.77 93.35 97.47 98.77 100.00
Individuals (the 10 first)
Dim.1 ctr cos2 Dim.2 ctr cos2
1 | -0.45 1.11 0.35 | -0.26 0.98 0.12 |
2 | 0.84 3.79 0.56 | -0.03 0.01 0.00 |
3 | -0.45 1.09 0.55 | 0.14 0.26 0.05 |
4 | 0.88 4.20 0.75 | -0.09 0.10 0.01 |
5 | -0.45 1.09 0.55 | 0.14 0.26 0.05 |
6 | -0.36 0.70 0.02 | -0.44 2.68 0.04 |
7 | -0.45 1.09 0.55 | 0.14 0.26 0.05 |
8 | -0.64 2.23 0.62 | -0.01 0.00 0.00 |
9 | -0.45 1.11 0.35 | -0.26 0.98 0.12 |
10 | -0.14 0.11 0.04 | 0.12 0.21 0.03 |
Categories (the 10 first)
Dim.1 ctr cos2 v.test Dim.2 ctr cos2 v.test
Nausea_n | 0.27 1.52 0.26 3.72 | 0.12 0.81 0.05 1.69 |
Nausea_y | -0.96 5.43 0.26 -3.72 | -0.43 2.91 0.05 -1.69 |
Vomit_n | 0.48 3.73 0.34 4.31 | -0.41 7.07 0.25 -3.68 |
Vomit_y | -0.72 5.60 0.34 -4.31 | 0.61 10.61 0.25 3.68 |
Abdo_n | 1.32 15.42 0.85 6.76 | -0.04 0.03 0.00 -0.18 |
Abdo_y | -0.64 7.50 0.85 -6.76 | 0.02 0.01 0.00 0.18 |
Fever_n | 1.17 13.54 0.78 6.51 | -0.17 0.78 0.02 -0.97 |
Fever_y | -0.67 7.74 0.78 -6.51 | 0.10 0.45 0.02 0.97 |
Diarrhea_n | 1.18 13.80 0.80 6.57 | 0.00 0.00 0.00 -0.02 |
Diarrhea_y | -0.68 7.88 0.80 -6.57 | 0.00 0.00 0.00 0.02 |
Categorical variables (eta2)
Dim.1 Dim.2
Nausea | 0.26 0.05 |
Vomiting | 0.34 0.25 |
Abdominals | 0.85 0.00 |
Fever | 0.78 0.02 |
Diarrhae | 0.80 0.00 |
Potato | 0.03 0.40 |
Fish | 0.01 0.03 |
Mayo | 0.38 0.03 |
Courgette | 0.02 0.45 |
Cheese | 0.19 0.05 |The result of the function summary() contains 4 tables:
- Table 1 - Eigenvalues: table 1 contains the variances and the percentage of variances retained by each dimension.
- Table 2 contains the coordinates, the contribution and the cos2 (quality of representation [in 0-1]) of the first 10 active individuals on the dimensions 1 and 2.
- Table 3 contains the coordinates, the contribution and the cos2 (quality of representation [in 0-1]) of the first 10 active variable categories on the dimensions 1 and 2. This table contains also a column called v.test. The value of the v.test is generally comprised between 2 and -2. For a given variable category, if the absolute value of the v.test is superior to 2, this means that the coordinate is significantly different from 0.
- Table 4 - categorical variables (eta2): contains the squared correlation between each variable and the dimensions.
- For exporting the summary to a file, use the code: summary(res.mca, file =myfile.txt)
- For displaying the summary of more than 10 elements, use the argument nbelements in the function summary()
Interpretation of MCA outputs
MCA results is interpreted as the results from a simple correspondence analysis (CA).
I recommend to read the interpretation of simple CA which has been comprehensively described in my previous post: Correspondence Analysis in R: The Ultimate Guide for the Analysis, the Visualization and the Interpretation.
Eigenvalues/variances and screeplot
The proportion of variances retained by the different dimensions (axes) can be extracted using the function get_eigenvalue() [in factoextra] as follow :
eigenvalues <- get_eigenvalue(res.mca)
head(round(eigenvalues, 2)) eigenvalue variance.percent cumulative.variance.percent
Dim.1 0.34 33.52 33.52
Dim.2 0.13 12.91 46.44
Dim.3 0.11 10.73 57.17
Dim.4 0.10 9.59 66.76
Dim.5 0.08 7.88 74.64
Dim.6 0.07 7.11 81.75The function fviz_screeplot() [in factoextra package] can be used to draw the scree plot (the percentages of inertia explained by the MCA dimensions):
fviz_screeplot(res.mca)
Read more about eigenvalues and screeplot: Eigenvalues data visualization
MCA scatter plot: Biplot of individuals and variable categories
The function plot.MCA() [in FactoMineR package] can be used. A simplified format is :
plot(x, axes = c(1,2), choix=c("ind", "var"))- x : An object of class MCA
- axes : A numeric vector of length 2 specifying the component to plot
- choix : The graph to be plotted. Possible values are ind for the individuals and var for the variables
FactoMineR base graph for MCA:
plot(res.mca)
Its also possible to use the function fviz_mca_biplot()[in factoextra package] to draw a nice looking plot:
fviz_mca_biplot(res.mca)
# Change the theme
fviz_mca_biplot(res.mca) +
theme_minimal()
Read more about fviz_mca_biplot(): fviz_mca_biplot
The graph above shows a global pattern within the data. Rows (individuals) are represented by blue points and columns (variable categories) by red triangles.
The distance between any row points or column points gives a measure of their similarity (or dissimilarity).
Row points with similar profile are closed on the factor map. The same holds true for column points.
Variable categories
The function get_mca_var()[in factoextra] is used to extract the results for variable categories. This function returns a list containing the coordinates, the cos2 and the contribution of variable categories:
var <- get_mca_var(res.mca)
varMultiple Correspondence Analysis Results for variables
===================================================
Name Description
1 "$coord" "Coordinates for categories"
2 "$cos2" "Cos2 for categories"
3 "$contrib" "contributions of categories"Correlation between variables and principal dimensions
Variables can be visualized as follow:
plot(res.mca, choix = "var")
The plot above helps to identify variables that are the most correlated with each dimension. The squared correlations between variables and the dimensions are used as coordinates.
- It can be seen that, the variables Diarrhae, Abdominals and Fever are the most correlated with dimension 1. Similarly, the variables Courgette and Potato are the most correlated with dimension 2.
Coordinates of variable categories
head(round(var$coord, 2)) Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
Nausea_n 0.27 0.12 -0.27 0.03 0.07
Nausea_y -0.96 -0.43 0.95 -0.12 -0.26
Vomit_n 0.48 -0.41 0.08 0.27 0.05
Vomit_y -0.72 0.61 -0.13 -0.41 -0.08
Abdo_n 1.32 -0.04 -0.01 -0.15 -0.07
Abdo_y -0.64 0.02 0.00 0.07 0.03Use the function fviz_mca_var() [in factoextra] to visualize only variable categories:
# Default plot
fviz_mca_var(res.mca)
Its possible to change the color and the shape of the variable points using the arguments col.var and shape.var as follow:
fviz_mca_var(res.mca, col.var="black", shape.var = 15)
Note that, its also possible to make the graph of variables only using FactoMineR base graph. The argument invisible is used to hide the individual points:
# Hide individuals
plot(res.mca, invisible="ind") Contribution of variable categories to the dimensions
The contribution of the variable categories (in %) to the definition of the dimensions can be extracted as follow:
head(round(var$contrib,2)) Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
Nausea_n 1.52 0.81 4.67 0.08 0.49
Nausea_y 5.43 2.91 16.73 0.30 1.76
Vomit_n 3.73 7.07 0.36 4.26 0.19
Vomit_y 5.60 10.61 0.54 6.39 0.29
Abdo_n 15.42 0.03 0.00 0.73 0.18
Abdo_y 7.50 0.01 0.00 0.36 0.09The variable categories with the larger value, contribute the most to the definition of the dimensions.
The different categories in the table are:
categories <- rownames(var$coord)
length(categories)[1] 22print(categories) [1] "Nausea_n" "Nausea_y" "Vomit_n" "Vomit_y" "Abdo_n" "Abdo_y" "Fever_n"
[8] "Fever_y" "Diarrhea_n" "Diarrhea_y" "Potato_n" "Potato_y" "Fish_n" "Fish_y"
[15] "Mayo_n" "Mayo_y" "Courg_n" "Courg_y" "Cheese_n" "Cheese_y" "Icecream_n"
[22] "Icecream_y"Its possible to use the function corrplot to highlight the most contributing variables for each dimension:
library("corrplot")
corrplot(var$contrib, is.corr = FALSE)
The function fviz_contrib()[in factoextra] can be used to draw a bar plot of variable contributions:
# Contributions of variables on Dim.1
fviz_contrib(res.mca, choice = "var", axes = 1)
If the contribution of variable categories were uniform, the expected value would be 1/number_of_categories = 1/22 = 4.5%.
- The red dashed line on the graph above indicates the expected average contribution. For a given dimension, any category with a contribution larger than this threshold could be considered as important in contributing to that dimension.
It can be seen that the categories Abdo_n, Diarrhea_n, Fever_n and Mayo_n are the most important in the definition of the first dimension.
# Contributions of rows on Dim.2
fviz_contrib(res.mca, choice = "var", axes = 2)
The row items Courg_n, Potato_n, Vomit_y and Icecream_n contribute the most to the dimension 2.
# Total contribution on Dim.1 and Dim.2
fviz_contrib(res.mca, choice = "var", axes = 1:2)
The total contribution of a category, on explaining the variations retained by Dim.1 and Dim.2, is calculated as follow : (C1 * Eig1) + (C2 * Eig2).
C1 and C2 are the contributions of the category to dimensions 1 and 2, respectively. Eig1 and Eig2 are the eigenvalues of dimensions 1 and 2, respectively.
The expected average contribution of a category for Dim.1 and Dim.2 is : (4.5 * Eig1) + (4.5 * Eig2) = (4.50.34) + (4.50.13) = 2.12%If your data contains many categories, the top contributing categories can be displayed as follow:
fviz_contrib(res.mca, choice = "var", axes = 1, top = 10)
Read more about fviz_contrib(): fviz_contrib
A second option is to draw a scatter plot of categories and to highlight categories according to the amount of their contributions. The function fviz_mca_var() is used.
Note that, using factoextra package, the color or the transparency of the variable categories can be automatically controlled by the value of their contributions, their cos2, their coordinates on x or y axis.
# Control category point colors using their contribution
# Possible values for the argument col.row are :
# "cos2", "contrib", "coord", "x", "y"
fviz_mca_var(res.mca, col.var = "contrib")
# Change the gradient color
fviz_mca_var(res.mca, col.var="contrib")+
scale_color_gradient2(low="white", mid="blue",
high="red", midpoint=2)+theme_minimal()
The scatter plot is also helpful to highlight the most important categories in the determination of the dimensions.
In addition we can have an idea of what pole of the dimensions the categories are actually contributing to.
It is evident that the categories Abdo_n, Diarrhea_n, Fever_n and Mayo_n have an important contribution to the positive pole of the first dimension, while the categories Fever_y and Diarrhea_y have a major contribution to the negative pole of the first dimension; etc, .Its also possible to control automatically the transparency of variable categories by their contributions. The argument alpha.var is used:
# Control the transparency of categories using their contribution
# Possible values for the argument alpha.var are :
# "cos2", "contrib", "coord", "x", "y"
fviz_mca_var(res.mca, alpha.var="contrib")+
theme_minimal()
Its possible to select and display only the top contributing categories as illustrated in the R code below.
# Select the top 10 contributing categories
fviz_mca_var(res.mca, select.var=list(contrib=10))
Variable category/individual selections are discussed in details in the next sections
Read more about fviz_mca_var(): fviz_mca_var
Cos2 : The quality of representation of variable categories
The two dimensions 1 and 2 are sufficient to retain 46% of the total inertia contained in the data.
However, not all the points are equally well displayed in the two dimensions.
The quality of representation of the categories on the factor map is called the squared cosine (cos2) or the squared correlations.
The cos2 measures the degree of association between variable categories and a particular axis.
The cos2 of variable categories can be extracted as follow:
head(var$cos2) Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
Nausea_n 0.2562007 0.0528025759 2.527485e-01 0.004084375 0.019466197
Nausea_y 0.2562007 0.0528025759 2.527485e-01 0.004084375 0.019466197
Vomit_n 0.3442016 0.2511603912 1.070855e-02 0.112294813 0.004126898
Vomit_y 0.3442016 0.2511603912 1.070855e-02 0.112294813 0.004126898
Abdo_n 0.8451157 0.0006215864 1.262496e-05 0.011479077 0.002374929
Abdo_y 0.8451157 0.0006215864 1.262496e-05 0.011479077 0.002374929The values of the cos2 are comprised between 0 and 1.
The sum of the cos2 for rows on all the MCA dimensions is equal to one.
The quality of representation of a variable category or an individual in n dimensions is simply the sum of the squared cosine of that variable category or individual over the n dimensions.
If a variable category is well represented by two dimensions, the sum of the cos2 is closed to one.
For some of the categories, more than 2 dimensions are required to perfectly represent the data.
Visualize the cos2 of variable categories using corrplot:
library("corrplot")
corrplot(var$cos2, is.corr=FALSE)
The function fviz_cos2()[in factoextra] can be used to draw a bar plot of rows cos2:
# Cos2 of variable categories on Dim.1 and Dim.2
fviz_cos2(res.mca, choice = "var", axes = 1:2)
Note that, variable categories Fish_n, Fish_y, Icecream_n and Icecream_y are not very well represented by the first two dimensions. This implies that the position of the corresponding points on the scatter plot should be interpreted with some caution. A higher dimensional solution is probably necessary.
Read more about fviz_cos2(): fviz_cos2
Individuals
The function get_mca_ind()[in factoextra] is used to extract the results for individuals. This function returns a list containing the coordinates, the cos2 and the contributions of individuals:
ind <- get_mca_ind(res.mca)
indMultiple Correspondence Analysis Results for individuals
===================================================
Name Description
1 "$coord" "Coordinates for the individuals"
2 "$cos2" "Cos2 for the individuals"
3 "$contrib" "contributions of the individuals"The result for individuals gives the same information as described for variable categories. For this reason, Ill just displayed the result for individuals in this section without commenting.
Coordinates of individuals
head(ind$coord) Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
1 -0.4525811 -0.26415072 0.17151614 0.01369348 -0.11696806
2 0.8361700 -0.03193457 -0.07208249 -0.08550351 0.51978710
3 -0.4481892 0.13538726 -0.22484048 -0.14170168 -0.05004753
4 0.8803694 -0.08536230 -0.02052044 -0.07275873 -0.22935022
5 -0.4481892 0.13538726 -0.22484048 -0.14170168 -0.05004753
6 -0.3594324 -0.43604390 -1.20932223 1.72464616 0.04348157Use the function fviz_mca_ind() [in factoextra] to visualize only column points:
fviz_mca_ind(res.mca)
Read more about fviz_mca_ind(): fviz_mca_ind
Note that, its also possible to make the graph of individuals only using FactoMineR base graph.The argument invisible is used to hide the variable categories on the factor map:
# Hide variable categories
plot(res.mca, invisible="var") Contribution of individuals to the dimensions
head(ind$contrib) Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
1 1.110927 0.98238297 0.498254685 0.003555817 0.31554778
2 3.792117 0.01435818 0.088003703 0.138637089 6.23134138
3 1.089470 0.25806722 0.856229950 0.380768961 0.05776914
4 4.203611 0.10259105 0.007132055 0.100387990 1.21319013
5 1.089470 0.25806722 0.856229950 0.380768961 0.05776914
6 0.700692 2.67693398 24.769968729 56.404214518 0.04360547Note that, you can use the previously mentioned corrplot() function to visualize the contribution of individuals.
Use the function fviz_contrib()[in factoextra] to visualize column contributions on dimensions 1+2:
fviz_contrib(res.mca, choice = "ind", axes = 1:2, top = 20)
If the individual contributions were uniform, the expected value would be 1/nrow(poison) = 1/55 = 1.8%.
- The expected average contribution (reference line) of a column for Dim.1 and Dim.2 is : (1.8 * Eig1) + (1.8 * Eig2) = (1.8 * 0.34) + (1.8 * 0.13) = 0.85%.
Draw a scatter plot of individuals points and highlight individuals according to the amount of their contributions. The function fviz_mca_ind() [in factoextra] is used:
# Control individual colors using their contribution
# Possible values for the argument col.ind are :
# "cos2", "contrib", "coord", "x", "y"
fviz_mca_ind(res.mca, col.ind="contrib")+
scale_color_gradient2(low="white", mid="blue",
high="red", midpoint=0.85)+theme_minimal()
Note that, its also possible to control automatically the transparency of individuals by their contributions using the argument alpha.ind:
# Control the transparency of individuals using their contribution
# Possible values for the argument alpha.ind are :
# "cos2", "contrib", "coord", "x", "y"
fviz_mca_ind(res.mca, alpha.ind="contrib")Cos2 : The quality of representation of individuals
head(ind$cos2) Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
1 0.34652591 0.1180447167 0.0497683175 0.0003172275 0.0231460846
2 0.55589562 0.0008108236 0.0041310808 0.0058126211 0.2148103098
3 0.54813888 0.0500176790 0.1379484860 0.0547920948 0.0068349171
4 0.74773962 0.0070299584 0.0004062504 0.0051072923 0.0507479873
5 0.54813888 0.0500176790 0.1379484860 0.0547920948 0.0068349171
6 0.02485357 0.0365775483 0.2813443706 0.5722083217 0.0003637178Note that, the value of the cos2 is between 0 and 1. A cos2 closed to 1 corresponds to a variable categories/individuals that are well represented on the factor map.
The function fviz_cos2()[in factoextra] can be used to draw a bar plot of individuals cos2:
# Cos2 of individuals on Dim.1 and Dim.2
fviz_cos2(res.mca, choice = "ind", axes = 1:2, top = 20)
Change the color of individuals by groups
As mentioned above, our data contains supplementary qualitative variables: Columns 3 and 4 corresponding to the columns Sick and Sex, respectively. These factor variables will be used to color individuals by groups.
sick <- as.factor(poison$Sick)
head(sick)[1] Sick_y Sick_n Sick_y Sick_n Sick_y Sick_y
Levels: Sick_n Sick_ysex <- as.factor(poison$Sex)
head(sex)[1] F F F F M M
Levels: F MIndividuals factor map :
# Default plot
fviz_mca_ind(res.mca, label ="none")
Change individual colors by groups using the levels of the variable sick. The argument habillage is used:
fviz_mca_ind(res.mca, label = "none", habillage=sick)
Add ellipses of point concentrations : the argument habillage is used to specify the factor variable for coloring the observations by groups.
fviz_mca_ind(res.mca, label="none", habillage = sick,
addEllipses = TRUE, ellipse.level = 0.95)
Now, lets :
- make a biplot of individuals and variable categories
- change the color of individuals by groups (sick levels)
- show only the labels for variables
fviz_mca_biplot(res.mca,
habillage = sick, addEllipses = TRUE,
label = "var", shape.var = 15) +
scale_color_brewer(palette="Dark2")+
theme_minimal()
Note that, its possible to color the individuals using any of the qualitative variable in the initial data table (poison)
Lets color the individuals by groups using the levels of the variable Vomiting:
fviz_mca_ind(res.mca,
habillage = poison$Vomiting, addEllipses = TRUE) +
scale_color_brewer(palette="Dark2")+
theme_minimal()
Its also possible to use the index of the column as follow (habillage = 2):
fviz_mca_ind(res.mca,
habillage = 2, addEllipses = TRUE) +
scale_color_brewer(palette="Dark2")+
theme_minimal()You can also use the function plotellipses() [in FactoMineR] to draw confidence ellipses around the categories. The simplified format is:
plotellipses(model, keepvar="all", axis =c(1,2))- model: object of class MCA or PCA
- keppvar: a boolean or numeric vector of indexes of variables or a character vector of names of variables. If keepvar is all, quali or quali.sup, variables which are plotted are all the categorical variables, only those which are used to compute the dimensions (active variables) or only the supplementary categorical variables. If keepvar is a numeric vector of indexes or a character vector of names of variables, only relevant variables are plotted.
plotellipses(res.mca, keepvar=1)
plotellipses(res.mca, keepvar=1:4)
plotellipses(res.mca, keepvar="Vomiting")
plotellipses(res.mca, keepvar=c("Vomiting", "Fever"))
plotellipses(res.mca, keepvar="all")
MCA using supplementary individuals and variables
As described above, the data set poison contains:
- supplementary continuous variables (quanti.sup = 1:2, columns 1 and 2 corresponding to the columns Sick and Sex, respectively)
- supplementary qualitative variables (quali.sup = 3:4, corresponding to the columns Sick and Sex, respectively). This factor variables are used to color individuals by groups
The data doesnt contain supplementary individuals. However for demonstration, well use the individuals 53:55 as supplementary individuals. The coordinates of these individuals will be predicted from the parameters of the MCA on the active individuals (1:52)
Supplementary variables and individuals are not used for the determination of the principal dimensions. Their coordinates are predicted using only the information provided by the performed multiple correspondence analysis on active variables/individuals.
To specify supplementary individuals and variables, the function MCA() can be used as follow :
MCA(X, ncp = 5, ind.sup = NULL,
quanti.sup=NULL, quali.sup=NULL, graph=TRUE, axes = c(1,2))- X : a data frame. Rows are individuals and columns are variables.
- ncp : number of dimensions kept in the final results.
- ind.sup : a numeric vector specifying the indexes of the supplementary individuals
- quanti.sup, quali.sup : a numeric vector specifying, respectively, the indexes of the quantitative and qualitative variables
- graph : a logical value. If TRUE a graph is displayed.
- axes : a vector of length 2 specifying the components to be plotted
Example of usage :
res.mca <- MCA(poison, ind.sup=53:55,
quanti.sup = 1:2, quali.sup = 3:4, graph=FALSE)The summary of the MCA is :
summary(res.mca, nb.dec = 2, ncp = 2)
Eigenvalues
Dim.1 Dim.2 Dim.3 Dim.4 Dim.5 Dim.6 Dim.7 Dim.8 Dim.9 Dim.10 Dim.11
Variance 0.33 0.13 0.11 0.10 0.09 0.07 0.06 0.06 0.04 0.01 0.01
% of var. 32.88 13.04 10.63 9.67 8.60 6.66 6.40 5.94 3.89 1.33 0.95
Cumulative % of var. 32.88 45.92 56.56 66.23 74.83 81.49 87.89 93.83 97.72 99.05 100.00
Individuals (the 10 first)
Dim.1 ctr cos2 Dim.2 ctr cos2
1 | -0.44 1.14 0.35 | -0.27 1.10 0.13 |
2 | 0.85 4.23 0.54 | -0.01 0.00 0.00 |
3 | -0.43 1.09 0.50 | 0.13 0.24 0.04 |
4 | 0.91 4.81 0.77 | -0.03 0.01 0.00 |
5 | -0.43 1.09 0.50 | 0.13 0.24 0.04 |
6 | -0.34 0.67 0.02 | -0.45 2.93 0.04 |
7 | -0.43 1.09 0.50 | 0.13 0.24 0.04 |
8 | -0.63 2.32 0.61 | -0.02 0.00 0.00 |
9 | -0.44 1.14 0.35 | -0.27 1.10 0.13 |
10 | -0.12 0.08 0.03 | 0.14 0.27 0.04 |
Supplementary individuals
Dim.1 cos2 Dim.2 cos2
53 | 1.08 0.36 | 0.52 0.08 |
54 | -0.12 0.03 | 0.14 0.04 |
55 | -0.43 0.50 | 0.13 0.04 |
Categories (the 10 first)
Dim.1 ctr cos2 v.test Dim.2 ctr cos2 v.test
Nausea_n | 0.29 1.78 0.28 3.77 | 0.13 0.94 0.06 1.72 |
Nausea_y | -0.97 5.94 0.28 -3.77 | -0.44 3.12 0.06 -1.72 |
Vomit_n | 0.46 3.56 0.33 4.13 | -0.39 6.57 0.24 -3.53 |
Vomit_y | -0.73 5.70 0.33 -4.13 | 0.63 10.51 0.24 3.53 |
Abdo_n | 1.32 15.80 0.85 6.58 | 0.02 0.01 0.00 0.12 |
Abdo_y | -0.64 7.68 0.85 -6.58 | -0.01 0.01 0.00 -0.12 |
Fever_n | 1.17 13.89 0.79 6.35 | -0.12 0.36 0.01 -0.65 |
Fever_y | -0.68 8.00 0.79 -6.35 | 0.07 0.21 0.01 0.65 |
Diarrhea_n | 1.26 15.31 0.85 6.57 | 0.04 0.04 0.00 0.20 |
Diarrhea_y | -0.67 8.10 0.85 -6.57 | -0.02 0.02 0.00 -0.20 |
Categorical variables (eta2)
Dim.1 Dim.2
Nausea | 0.28 0.06 |
Vomiting | 0.33 0.24 |
Abdominals | 0.85 0.00 |
Fever | 0.79 0.01 |
Diarrhae | 0.85 0.00 |
Potato | 0.03 0.40 |
Fish | 0.01 0.03 |
Mayo | 0.33 0.04 |
Courgette | 0.02 0.48 |
Cheese | 0.13 0.03 |
Supplementary categories
Dim.1 cos2 v.test Dim.2 cos2 v.test
Sick_n | 1.42 0.89 6.75 | 0.00 0.00 0.01 |
Sick_y | -0.63 0.89 -6.75 | 0.00 0.00 -0.01 |
F | -0.03 0.00 -0.23 | 0.11 0.01 0.83 |
M | 0.03 0.00 0.23 | -0.12 0.01 -0.83 |
Supplementary categorical variables (eta2)
Dim.1 Dim.2
Sick | 0.89 0.00 |
Sex | 0.00 0.01 |
Supplementary continuous variables
Dim.1 Dim.2
Age | 0.00 | -0.01 |
Time | -0.84 | -0.08 |For the supplementary individuals/variable categories, the coordinates and the quality of representation (cos2) on the factor maps are shown. They dont contribute to the dimensions.
Make a biplot of individuals and variable categories
FactomineR base graph:
plot(res.mca)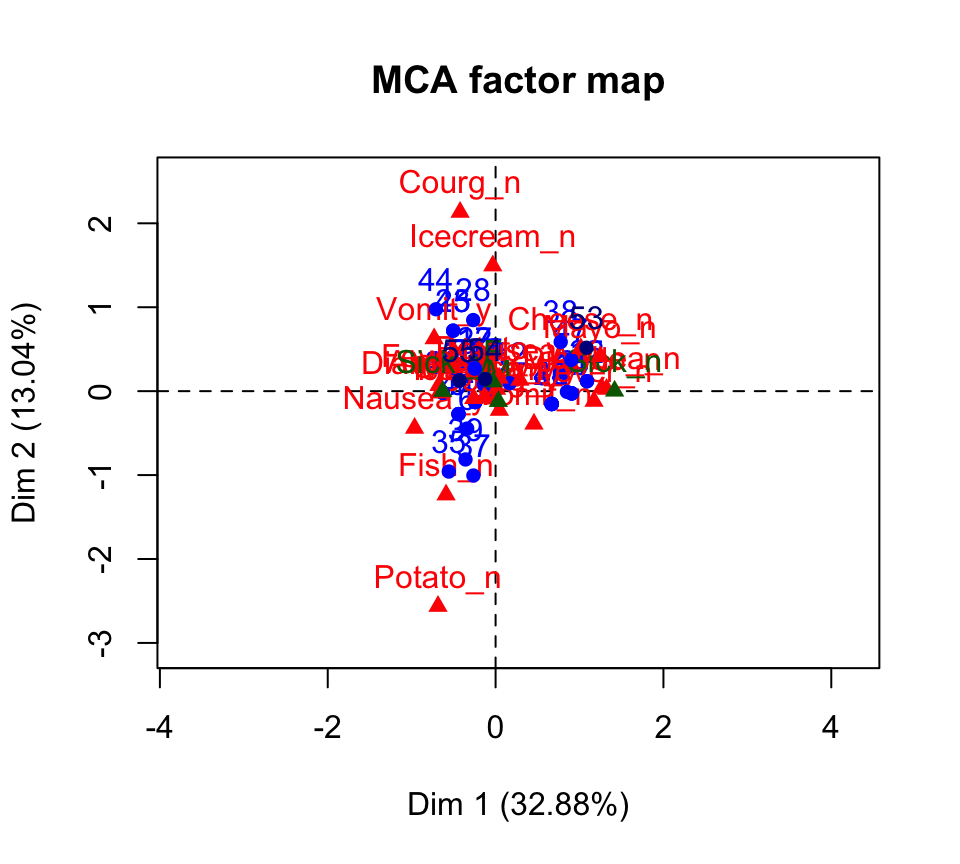
- Active individuals are in blue
- Supplementary individuals are in darkblue
- Active variable categories are in red
- Supplementary variable categories are in darkgreen
Use factoextra:
fviz_mca_biplot(res.mca) +
theme_minimal()
Visualize supplementary variables
The graph below highlight the correlation between variables (active & supplementary) and dimensions:
plot(res.mca, choix ="var")
Supplementary qualitative variable categories
All the results (coordinates, cos2, v.test and eta2) for the supplementary qualitative variable categories can be extracted as follow :
res.mca$quali.sup$coord
Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
Sick_n 1.41809140 0.0020394048 0.13199139 -0.016036841 -0.08354663
Sick_y -0.63026284 -0.0009064021 -0.05866284 0.007127485 0.03713184
F -0.03108147 0.1123143957 0.05033124 -0.055927173 -0.06832928
M 0.03356798 -0.1212995474 -0.05435774 0.060401347 0.07379562
$cos2
Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
Sick_n 0.893770319 1.848521e-06 0.007742990 0.0001143023 0.003102240
Sick_y 0.893770319 1.848521e-06 0.007742990 0.0001143023 0.003102240
F 0.001043342 1.362369e-02 0.002735892 0.0033780765 0.005042401
M 0.001043342 1.362369e-02 0.002735892 0.0033780765 0.005042401
$v.test
Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
Sick_n 6.7514655 0.009709509 0.6284047 -0.07635063 -0.3977615
Sick_y -6.7514655 -0.009709509 -0.6284047 0.07635063 0.3977615
F -0.2306739 0.833551410 0.3735378 -0.41506855 -0.5071119
M 0.2306739 -0.833551410 -0.3735378 0.41506855 0.5071119
$eta2
Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
Sick 0.893770319 1.848521e-06 0.007742990 0.0001143023 0.003102240
Sex 0.001043342 1.362369e-02 0.002735892 0.0033780765 0.005042401Factor map :
fviz_mca_var(res.mca) + theme_minimal()
# Hide active variables
fviz_mca_var(res.mca, invisible ="var") +
theme_minimal()
# Hide supplementary qualitative variables
fviz_mca_var(res.mca, invisible ="quali.sup") +
theme_minimal()
Supplementary variable categories are shown in darkgreen color.
Supplementary quantitative variables
The coordinates of supplementary quantitative variables are:
res.mca$quanti$coord
Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
Age 0.003934896 -0.00741340 -0.26494536 0.20015501 0.02928483
Time -0.838158507 -0.08330586 -0.08718851 -0.08421599 -0.02316931Graph using FactoMineR base graph:
plot(res.mca, choix="quanti.sup")
Visualize supplementary individuals
The results for supplementary individuals can be extracted as follow :
res.mca$ind.sup$coord
Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
53 1.0835684 0.5172478 0.5794063 0.5390903 0.4553650
54 -0.1249473 0.1417271 -0.1765234 -0.1526587 -0.2779565
55 -0.4315948 0.1270468 -0.2071580 -0.1186804 -0.1891760
$cos2
Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
53 0.36304957 0.08272764 0.10380536 0.08986204 0.06411692
54 0.03157652 0.04062716 0.06302535 0.04713607 0.15626590
55 0.50232519 0.04352713 0.11572730 0.03798314 0.09650827Factor map for individuals:
fviz_mca_ind(res.mca) +
theme_minimal()
# Show the label of ind.sup only
fviz_mca_ind(res.mca, label="ind.sup") +
theme_minimal()
Supplementary individuals are shown in darkblue.
Filter the MCA result
If you have many individuals/variable categories, its possible to visualize only some of them using the arguments select.ind and select.var.
select.ind, select.var: a selection of individuals/variable categories to be drawn. Allowed values are NULL or a list containing the arguments name, cos2 or contrib:
- name: is a character vector containing individuals/variable category names to be drawn
- cos2: if cos2 is in [0, 1], ex: 0.6, then individuals/variable categories with a cos2 > 0.6 are drawn
- if cos2 > 1, ex: 5, then the top 5 active individuals/variable categories and top 5 supplementary columns/rows with the highest cos2 are drawn
- contrib: if contrib > 1, ex: 5, then the top 5 individuals/variable categories with the highest cos2 are drawn
# Visualize variable categories with cos2 >= 0.4
fviz_mca_var(res.mca, select.var = list(cos2 = 0.4))
# Top 10 active variables with the highest cos2
fviz_mca_var(res.mca, select.var= list(cos2 = 10))
The top 10 active individuals and the top 10 supplementary individuals are shown.
# Select by names
name <- list(name = c("Fever_n", "Abdo_y", "Diarrhea_n", "Fever_Y", "Vomit_y", "Vomit_n"))
fviz_mca_var(res.mca, select.var = name)
#top 5 contributing individuals and variable categories
fviz_mca_biplot(res.mca, select.ind = list(contrib = 5),
select.var = list(contrib = 5)) +
theme_minimal()
Supplementary individuals/variable categories are not shown because they dont contribute to the construction of the axes.
Dimension description
The function dimdesc() can be used to identify the most correlated variables with a given dimension.
A simplified format is :
dimdesc(res, axes = 1:2, proba = 0.05)- res : an object of class MCA
- axes : a numeric vector specifying the dimensions to be described
- prob : the significance level
Example of usage :
res.desc <- dimdesc(res.mca, axes = c(1,2))
# Description of dimension 1
res.desc$`Dim 1`$quanti
correlation p.value
Time -0.8381585 9.12658e-15
$quali
R2 p.value
Sick 0.8937703 5.368221e-26
Abdominals 0.8493262 3.429439e-22
Diarrhae 0.8467702 5.229788e-22
Fever 0.7916690 1.168654e-18
Vomiting 0.3348718 7.001487e-06
Mayo 0.3257425 9.967995e-06
Nausea 0.2794053 5.623583e-05
Cheese 0.1344785 7.495656e-03
$category
Estimate p.value
Sick_n 0.5872910 5.368221e-26
Abdo_n 0.5632879 3.429439e-22
Diarrhea_n 0.5545730 5.229788e-22
Fever_n 0.5297728 1.168654e-18
Vomit_n 0.3410366 7.001487e-06
Mayo_n 0.4325471 9.967995e-06
Nausea_n 0.3597065 5.623583e-05
Cheese_n 0.3290968 7.495656e-03
Cheese_y -0.3290968 7.495656e-03
Nausea_y -0.3597065 5.623583e-05
Mayo_y -0.4325471 9.967995e-06
Vomit_y -0.3410366 7.001487e-06
Fever_y -0.5297728 1.168654e-18
Diarrhea_y -0.5545730 5.229788e-22
Abdo_y -0.5632879 3.429439e-22
Sick_y -0.5872910 5.368221e-26# Description of dimension 2
res.desc$`Dim 2`$quali
R2 p.value
Courgette 0.4839477 1.039252e-08
Potato 0.4020987 4.489421e-07
Vomiting 0.2449186 1.917736e-04
Icecream 0.1366683 6.989716e-03
$category
Estimate p.value
Courg_n 0.4261065 1.039252e-08
Potato_y 0.4910893 4.489421e-07
Vomit_y 0.1836850 1.917736e-04
Icecream_n 0.2863045 6.989716e-03
Icecream_y -0.2863045 6.989716e-03
Vomit_n -0.1836850 1.917736e-04
Potato_n -0.4910893 4.489421e-07
Courg_y -0.4261065 1.039252e-08Infos
This analysis has been performed using R software (ver. 3.2.1), FactoMineR (ver. 1.30) and factoextra (ver. 1.0.2)
References and further reading
- Bendixen M.1995, Compositional perceptual mapping using chi-squared tree analysis and Correspondence Analysis, «Journal of Marketing Management», 11, 571-581.
- Bendixen M. 2003, A Practical Guide to the Use of Correspondence Analysis in Marketing Research, Marketing Bulletin, 2003, 14, Technical Note 2. http://marketing-bulletin.massey.ac.nz/V14/MB_V14_T2_Bendixen.pdf
- Greenacre M.. Contribution biplots. http://www.econ.upf.edu/docs/papers/downloads/1162.pdf
- François Husson, http://factominer.free.fr/contact/index.html
