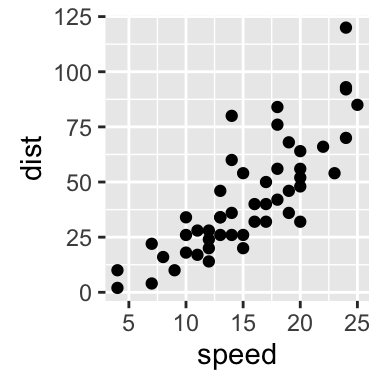
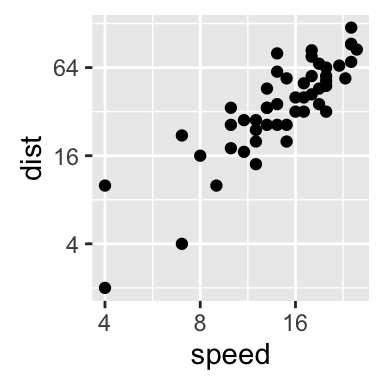
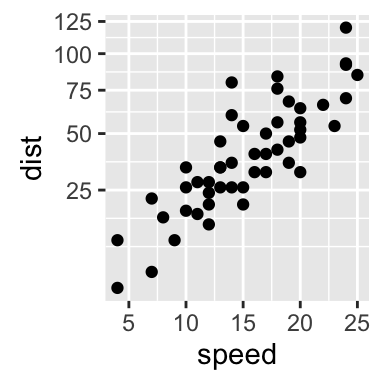
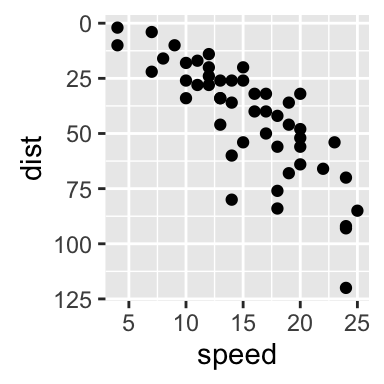
To arrange multiple ggplot2 graphs on the same page, the standard R functions - par() and layout() - cannot be used.
This R tutorial will show you, step by step, how to put several ggplots on a single page.
The functions grid.arrange()[in the package gridExtra] and plot_grid()[in the package cowplot], will be used.
Install and load required packages
Install and load the package gridExtra
install.packages("gridExtra")
library("gridExtra")Install and load the package cowplot
cowplot can be installed as follow:
install.packages("cowplot")OR
as follow using devtools package (devtools should be installed before using the code below):
devtools::install_github("wilkelab/cowplot")Load cowplot:
library("cowplot")Prepare some data
ToothGrowth data is used :
df <- ToothGrowth
# Convert the variable dose from a numeric to a factor variable
df$dose <- as.factor(df$dose)
head(df)## len supp dose
## 1 4.2 VC 0.5
## 2 11.5 VC 0.5
## 3 7.3 VC 0.5
## 4 5.8 VC 0.5
## 5 6.4 VC 0.5
## 6 10.0 VC 0.5Cowplot: Publication-ready plots
The cowplot package is an extension to ggplot2 and it can be used to provide a publication-ready plots.
Basic plots
library(cowplot)
# Default plot
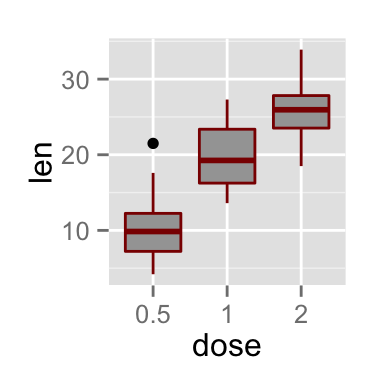
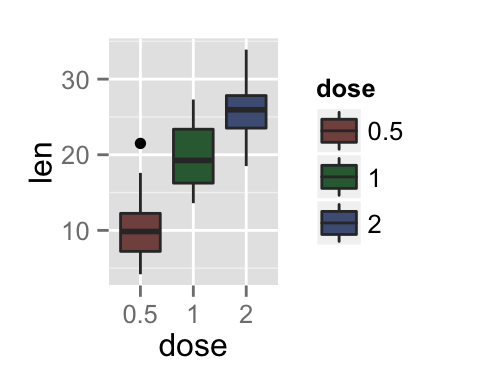
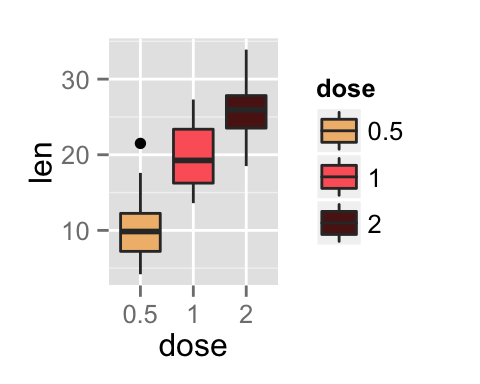
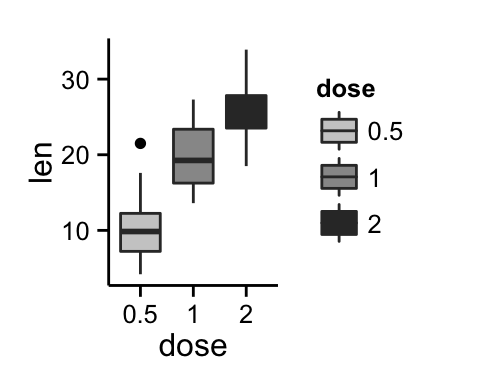
bp <- ggplot(df, aes(x=dose, y=len, color=dose)) +
geom_boxplot() +
theme(legend.position = "none")
bp
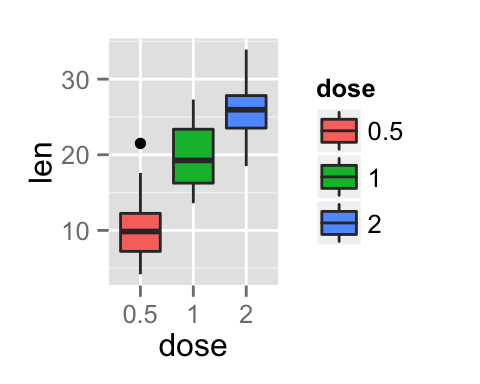
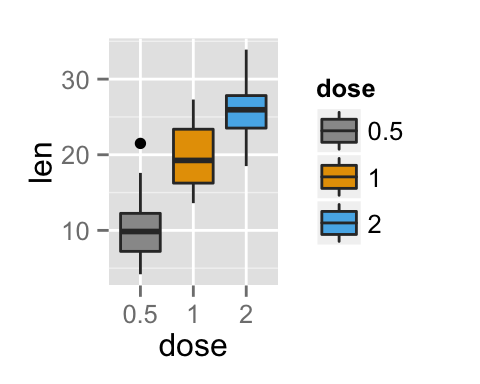
# Add gridlines
bp + background_grid(major = "xy", minor = "none")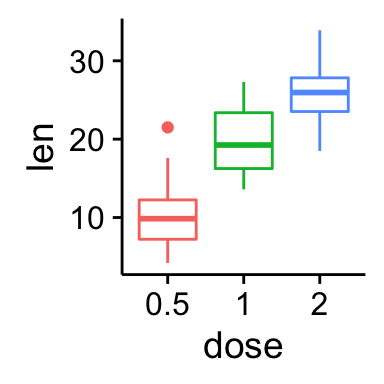
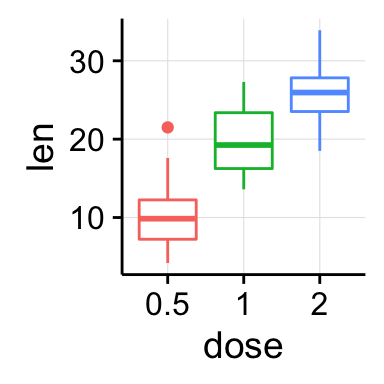
Recall that, the function ggsave()[in ggplot2 package] can be used to save ggplots. However, when working with cowplot, the function save_plot() [in cowplot package] is preferred. Its an alternative to ggsave with a better support for multi-figure plots.
save_plot("mpg.pdf", plot.mpg,
base_aspect_ratio = 1.3 # make room for figure legend
)Arranging multiple graphs using cowplot
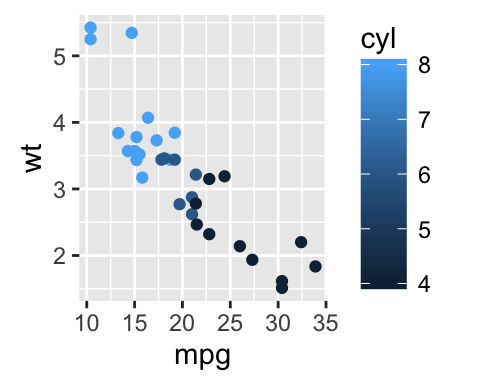
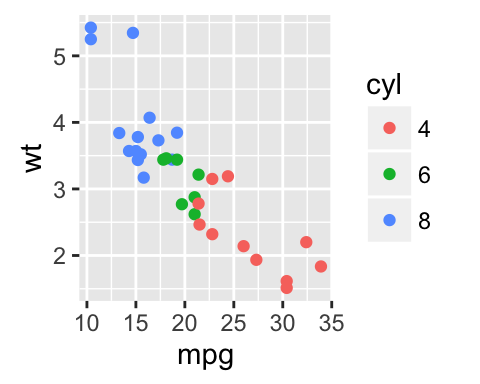
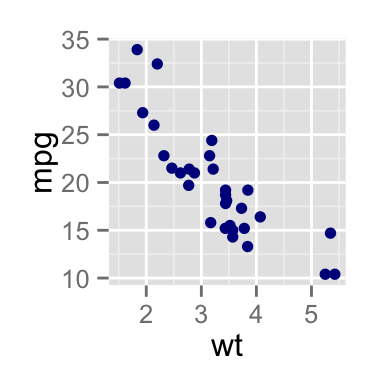
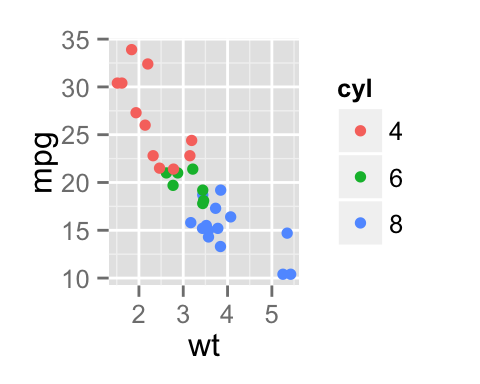
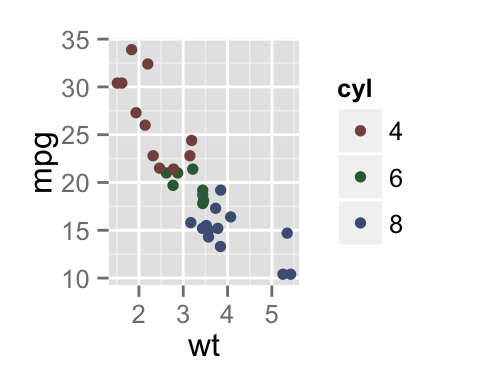
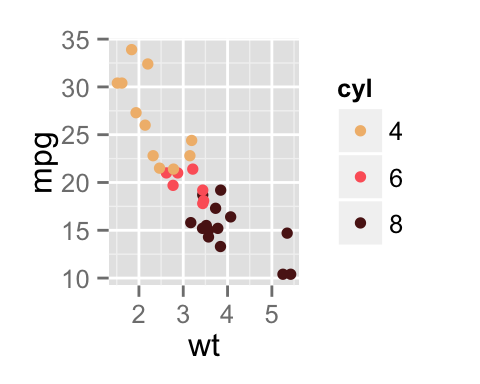
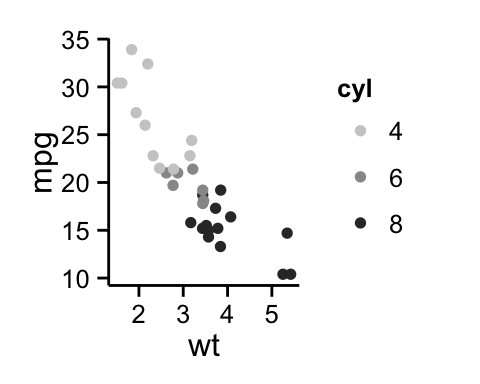
# Scatter plot
sp <- ggplot(mpg, aes(x = cty, y = hwy, colour = factor(cyl)))+
geom_point(size=2.5)
sp
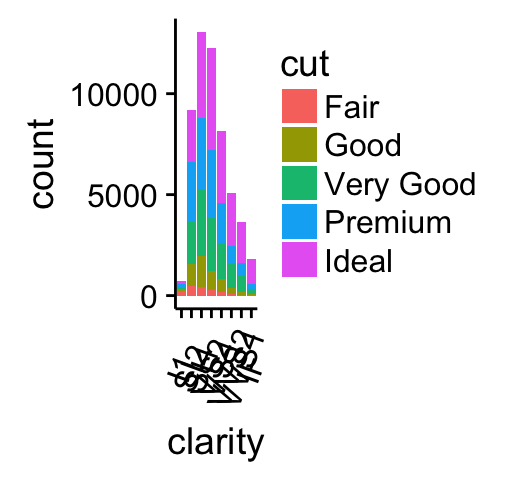
# Bar plot
bp <- ggplot(diamonds, aes(clarity, fill = cut)) +
geom_bar() +
theme(axis.text.x = element_text(angle=70, vjust=0.5))
bp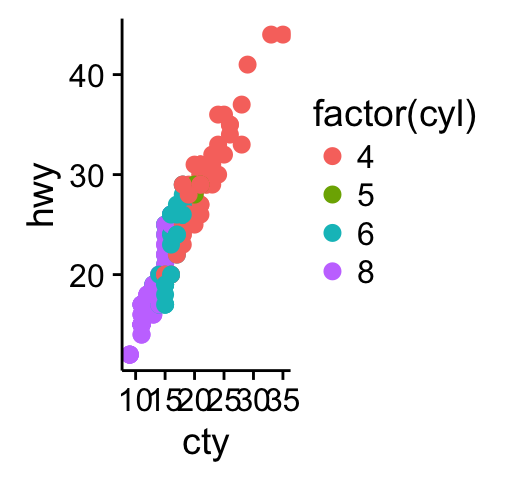
Combine the two plots (the scatter plot and the bar plot):
plot_grid(sp, bp, labels=c("A", "B"), ncol = 2, nrow = 1)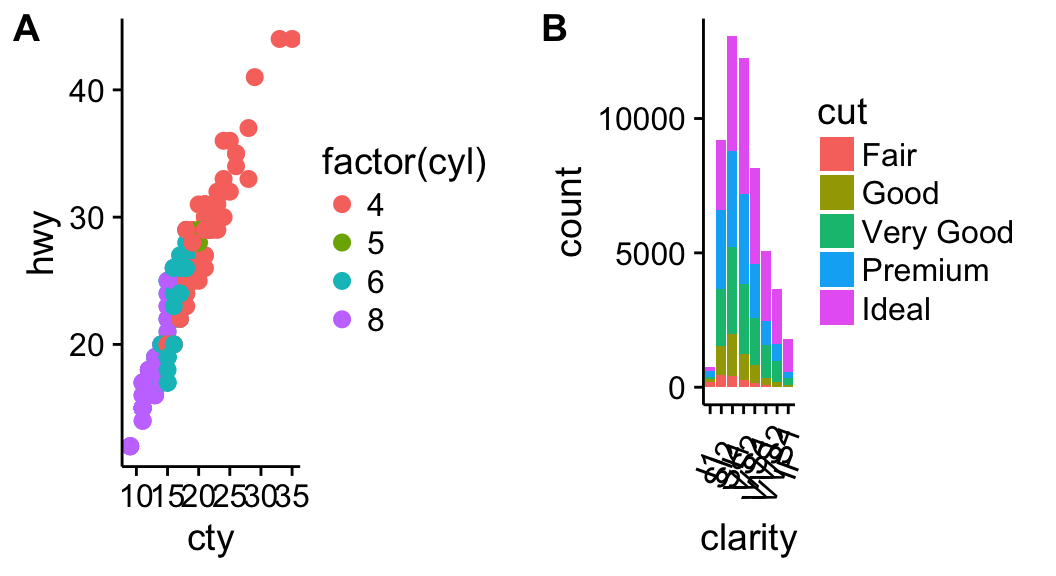
The function draw_plot() can be used to place graphs at particular locations with a particular sizes. The format of the function is:
draw_plot(plot, x = 0, y = 0, width = 1, height = 1)- plot: the plot to place (ggplot2 or a gtable)
- x: The x location of the lower left corner of the plot.
- y: The y location of the lower left corner of the plot.
- width, height: the width and the height of the plot
The function ggdraw() is used to initialize an empty drawing canvas.
plot.iris <- ggplot(iris, aes(Sepal.Length, Sepal.Width)) +
geom_point() + facet_grid(. ~ Species) + stat_smooth(method = "lm") +
background_grid(major = 'y', minor = "none") + # add thin horizontal lines
panel_border() # and a border around each panel
# plot.mpt and plot.diamonds were defined earlier
ggdraw() +
draw_plot(plot.iris, 0, .5, 1, .5) +
draw_plot(sp, 0, 0, .5, .5) +
draw_plot(bp, .5, 0, .5, .5) +
draw_plot_label(c("A", "B", "C"), c(0, 0, 0.5), c(1, 0.5, 0.5), size = 15)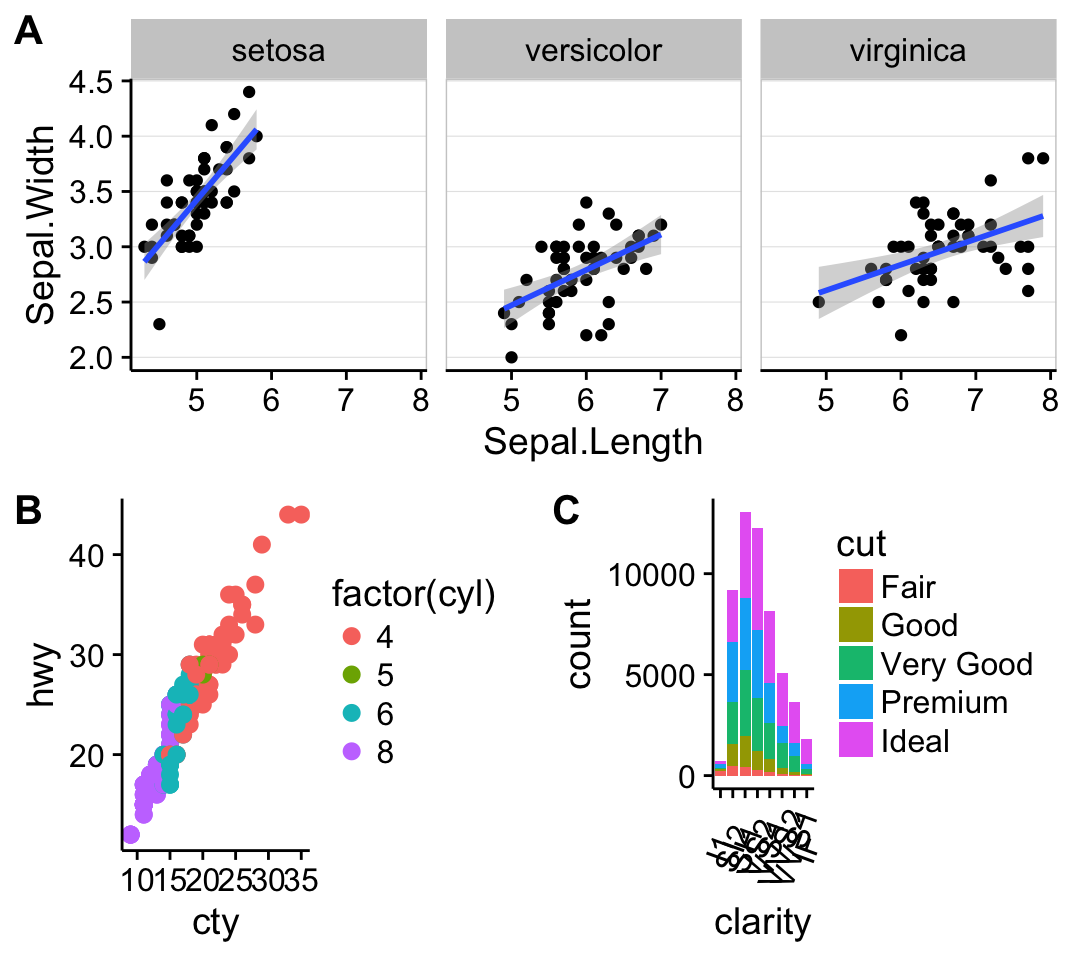
grid.arrange: Create and arrange multiple plots
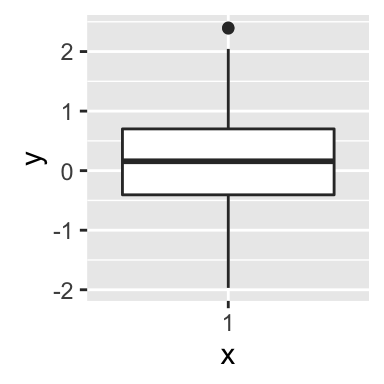
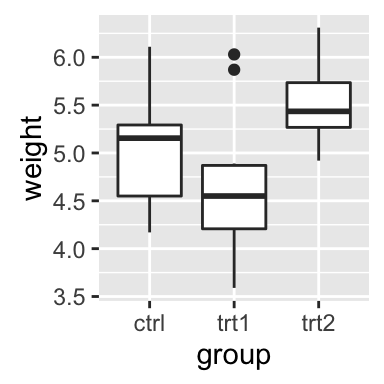
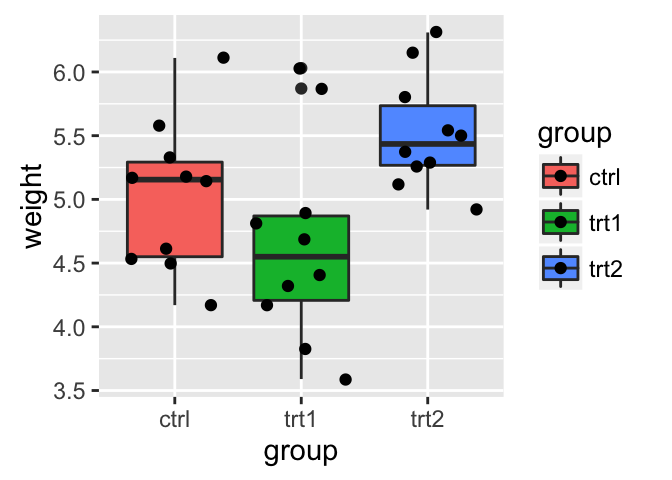
The R code below creates a box plot, a dot plot, a violin plot and a strip chart (jitter plot) :
library(ggplot2)
# Create a box plot
bp <- ggplot(df, aes(x=dose, y=len, color=dose)) +
geom_boxplot() +
theme(legend.position = "none")
# Create a dot plot
# Add the mean point and the standard deviation
dp <- ggplot(df, aes(x=dose, y=len, fill=dose)) +
geom_dotplot(binaxis='y', stackdir='center')+
stat_summary(fun.data=mean_sdl, mult=1,
geom="pointrange", color="red")+
theme(legend.position = "none")
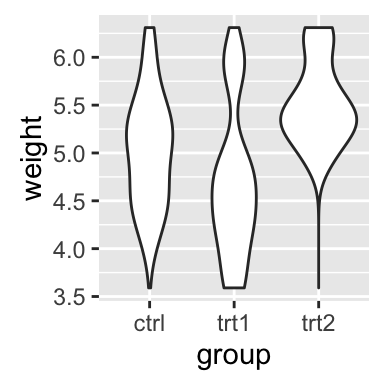
# Create a violin plot
vp <- ggplot(df, aes(x=dose, y=len)) +
geom_violin()+
geom_boxplot(width=0.1)
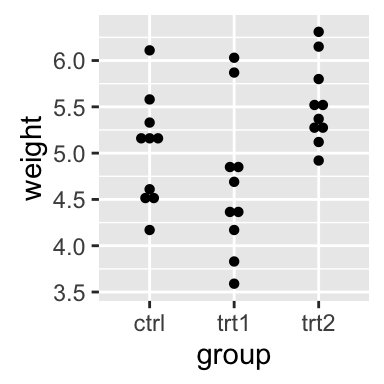
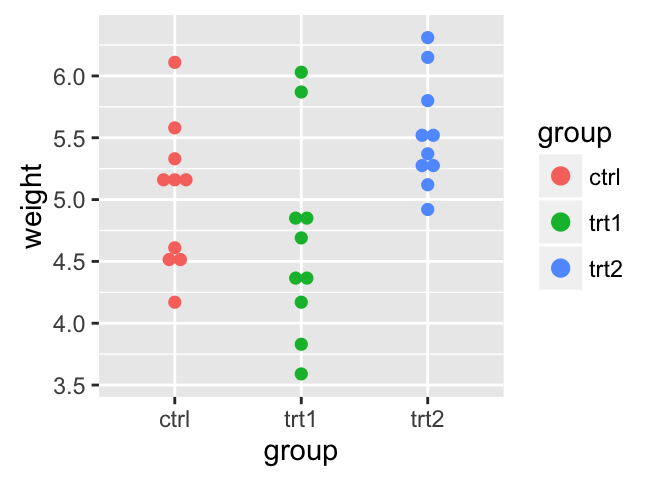
# Create a stripchart
sc <- ggplot(df, aes(x=dose, y=len, color=dose, shape=dose)) +
geom_jitter(position=position_jitter(0.2))+
theme(legend.position = "none") +
theme_gray()Combine the plots using the function grid.arrange() [in gridExtra] :
library(gridExtra)
grid.arrange(bp, dp, vp, sc, ncol=2, nrow =2)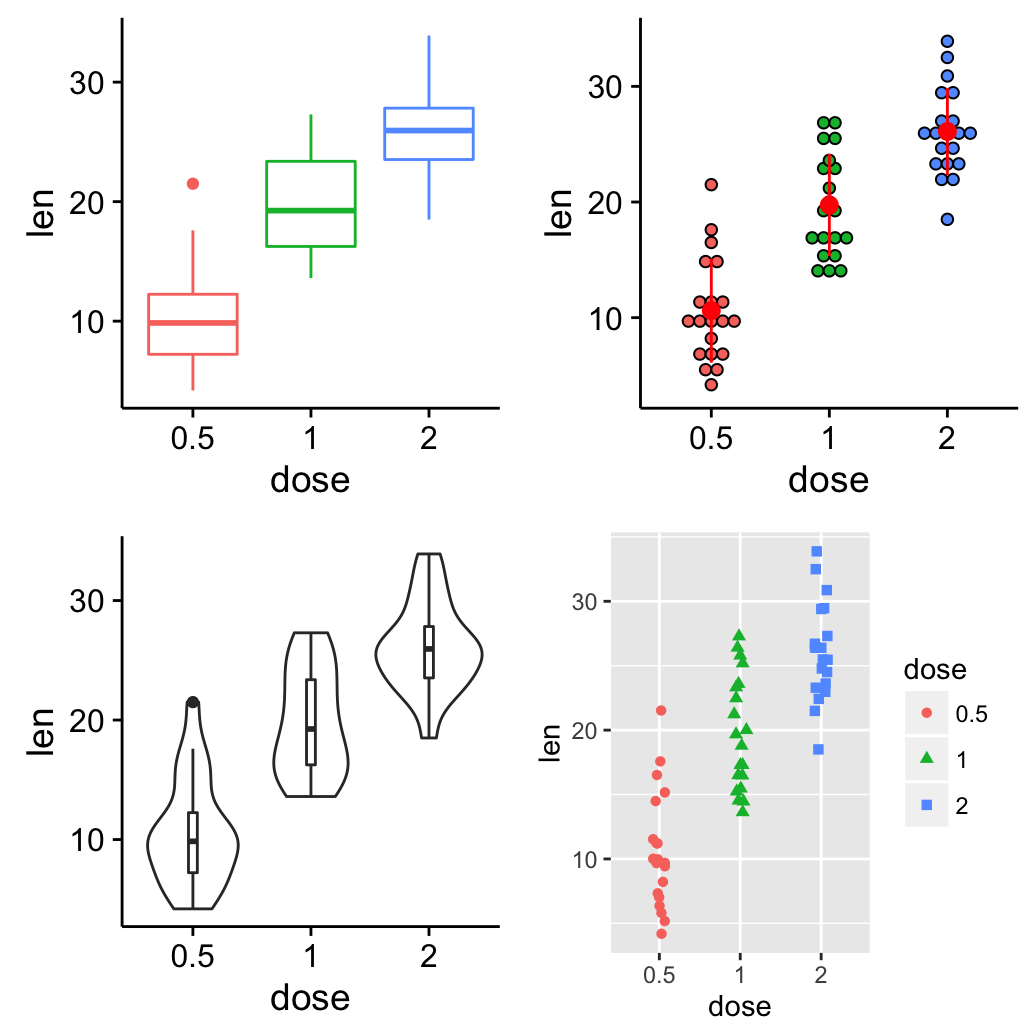
grid.arrange() and arrangeGrob(): Change column/row span of a plot
Using the R code below:
- The box plot will live in the first column
- The dot plot and the strip chart will live in the second column
grid.arrange(bp, arrangeGrob(dp, sc), ncol = 2)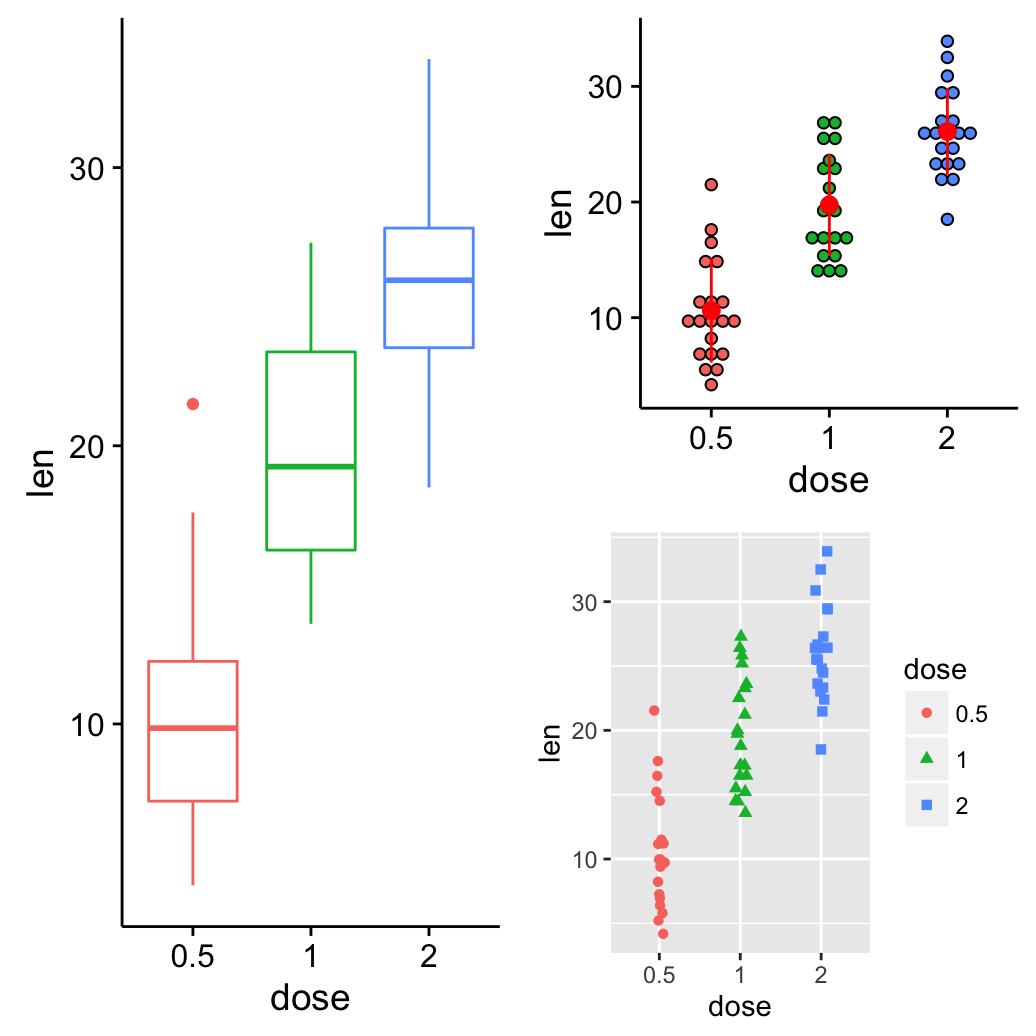
Its also possible to use the argument layout_matrix in grid.arrange(). In the R code below layout_matrix is a 2X3 matrix (2 columns and three rows). The first column is all 1s, thats where the first plot lives, spanning the three rows; second column contains plots 2, 3, 4, each occupying one row.
grid.arrange(bp, dp, sc, vp, ncol = 2,
layout_matrix = cbind(c(1,1,1), c(2,3,4)))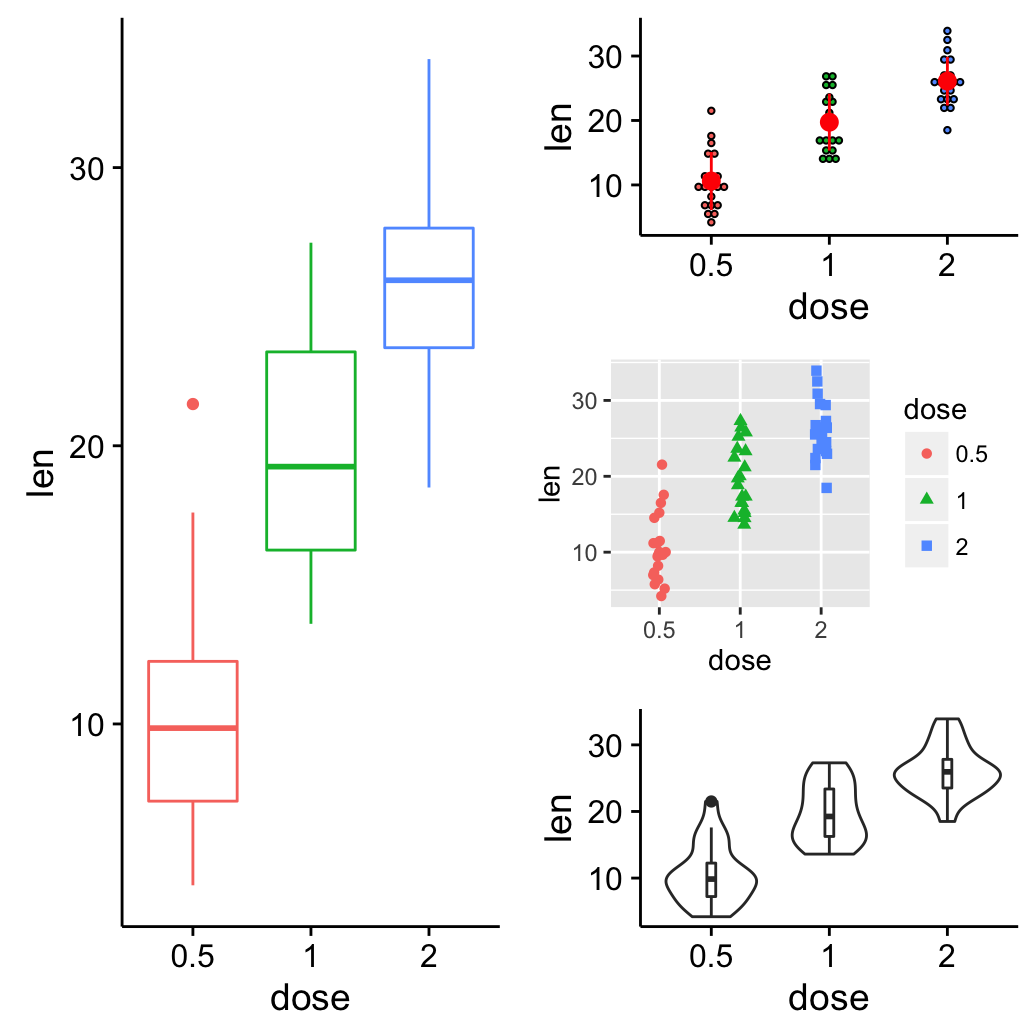
Add a common legend for multiple ggplot2 graphs
This can be done in four simple steps :
- Create the plots : p1, p2, .
- Save the legend of the plot p1 as an external graphical element (called a grob in Grid terminology)
- Remove the legends from all plots
- Draw all the plots with only one legend in the right panel
To save the legend of a ggplot, the helper function below can be used :
library(gridExtra)
get_legend<-function(myggplot){
tmp <- ggplot_gtable(ggplot_build(myggplot))
leg <- which(sapply(tmp$grobs, function(x) x$name) == "guide-box")
legend <- tmp$grobs[[leg]]
return(legend)
}(The function above is derived from this forum. )
# 1. Create the plots
#++++++++++++++++++++++++++++++++++
# Create a box plot
bp <- ggplot(df, aes(x=dose, y=len, color=dose)) +
geom_boxplot()
# Create a violin plot
vp <- ggplot(df, aes(x=dose, y=len, color=dose)) +
geom_violin()+
geom_boxplot(width=0.1)+
theme(legend.position="none")
# 2. Save the legend
#+++++++++++++++++++++++
legend <- get_legend(bp)
# 3. Remove the legend from the box plot
#+++++++++++++++++++++++
bp <- bp + theme(legend.position="none")
# 4. Arrange ggplot2 graphs with a specific width
grid.arrange(bp, vp, legend, ncol=3, widths=c(2.3, 2.3, 0.8))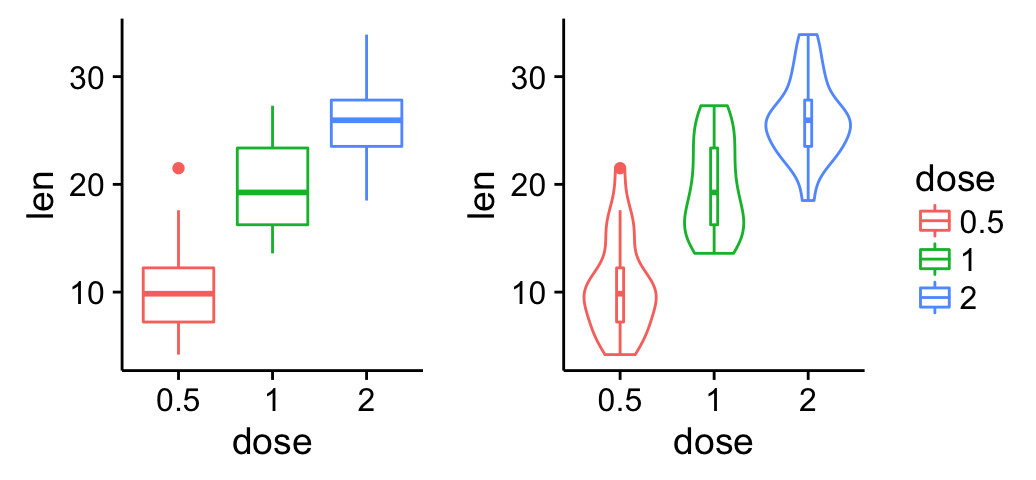
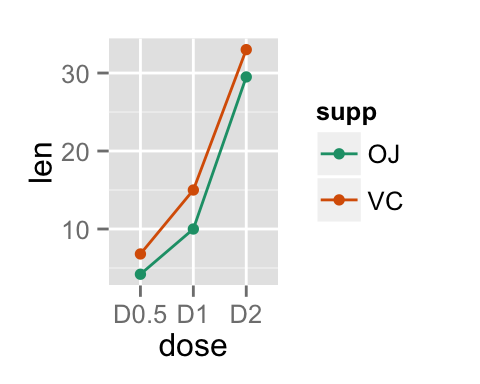
Change legend position
# 1. Create the plots
#++++++++++++++++++++++++++++++++++
# Create a box plot with a top legend position
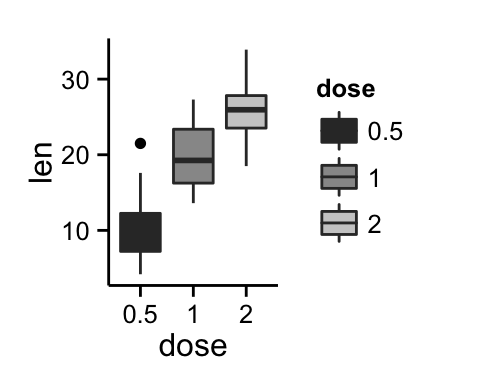
bp <- ggplot(df, aes(x=dose, y=len, color=dose)) +
geom_boxplot()+theme(legend.position = "top")
# Create a violin plot
vp <- ggplot(df, aes(x=dose, y=len, color=dose)) +
geom_violin()+
geom_boxplot(width=0.1)+
theme(legend.position="none")
# 2. Save the legend
#+++++++++++++++++++++++
legend <- get_legend(bp)
# 3. Remove the legend from the box plot
#+++++++++++++++++++++++
bp <- bp + theme(legend.position="none")
# 4. Create a blank plot
blankPlot <- ggplot()+geom_blank(aes(1,1)) +
cowplot::theme_nothing()Change legend position by changing the order of plots using the following R code. Grids with four cells are created (2X2). The height of the legend zone is set to 0.2.
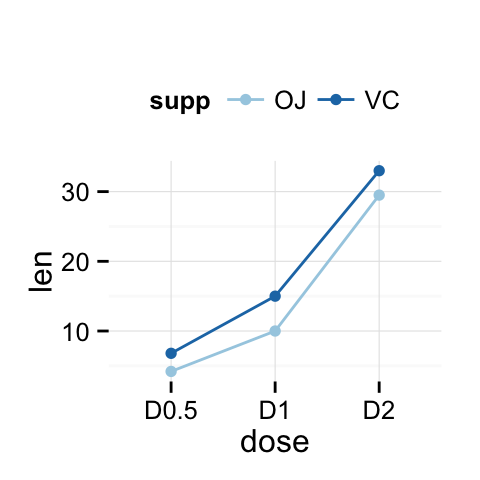
Top-left legend:
| Top-left legend | Blank plot |
| box plot | Violin plot |
# Top-left legend
grid.arrange(legend, blankPlot, bp, vp,
ncol=2, nrow = 2,
widths = c(2.7, 2.7), heights = c(0.2, 2.5))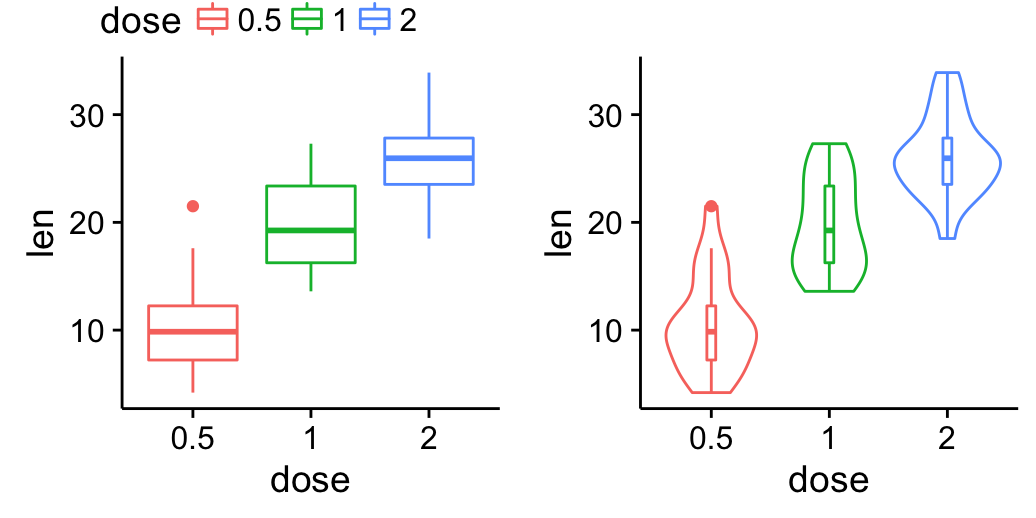
Top-right legend:
| Blank plot | Top right legend |
| box plot | Violin plot |
# Top-right
grid.arrange(blankPlot, legend, bp, vp,
ncol=2, nrow = 2,
widths = c(2.7, 2.7), heights = c(0.2, 2.5))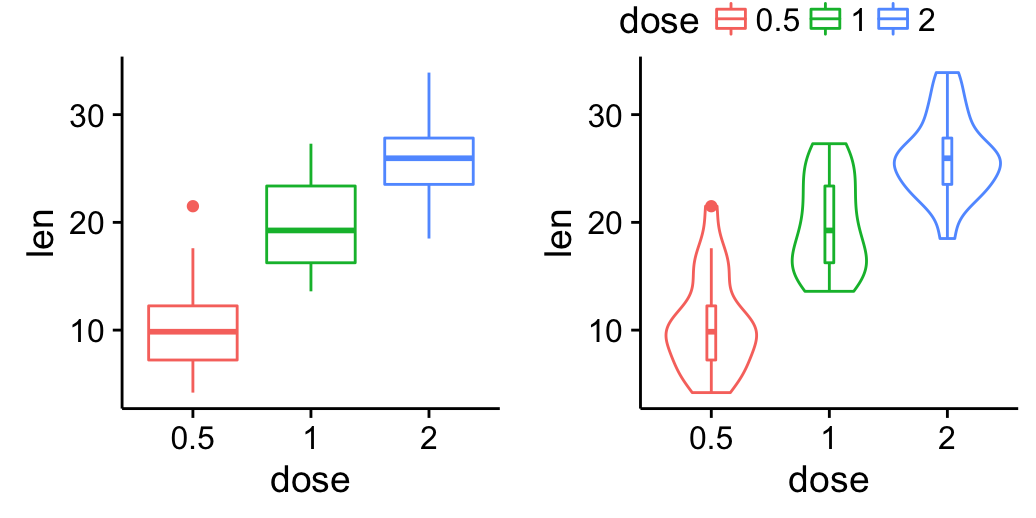
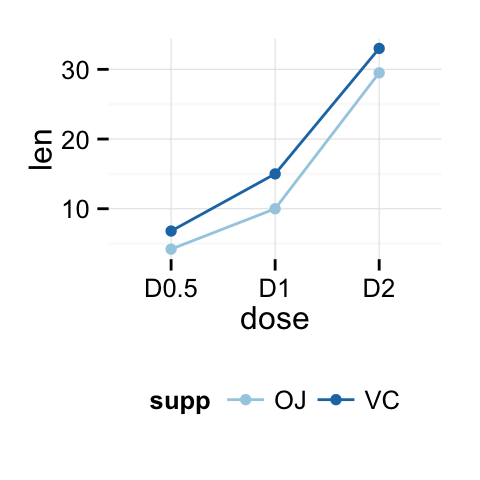
Bottom-right and bottom-left legend can be drawn as follow:
# Bottom-left legend
grid.arrange(bp, vp, legend, blankPlot,
ncol=2, nrow = 2,
widths = c(2.7, 2.7), heights = c(2.5, 0.2))
# Bottom-right
grid.arrange( bp, vp, blankPlot, legend,
ncol=2, nrow = 2,
widths = c(2.7, 2.7), heights = c( 2.5, 0.2))Its also possible to use the argument layout_matrix to customize legend position. In the R code below, layout_matrix is a 2X2 matrix:
- The first row (height = 2.5) is where the first plot (bp) and the second plot (vp) live
- The second row (height = 0.2) is where the legend lives spanning 2 columns
Bottom-center legend:
grid.arrange(bp, vp, legend, ncol=2, nrow = 2,
layout_matrix = rbind(c(1,2), c(3,3)),
widths = c(2.7, 2.7), heights = c(2.5, 0.2))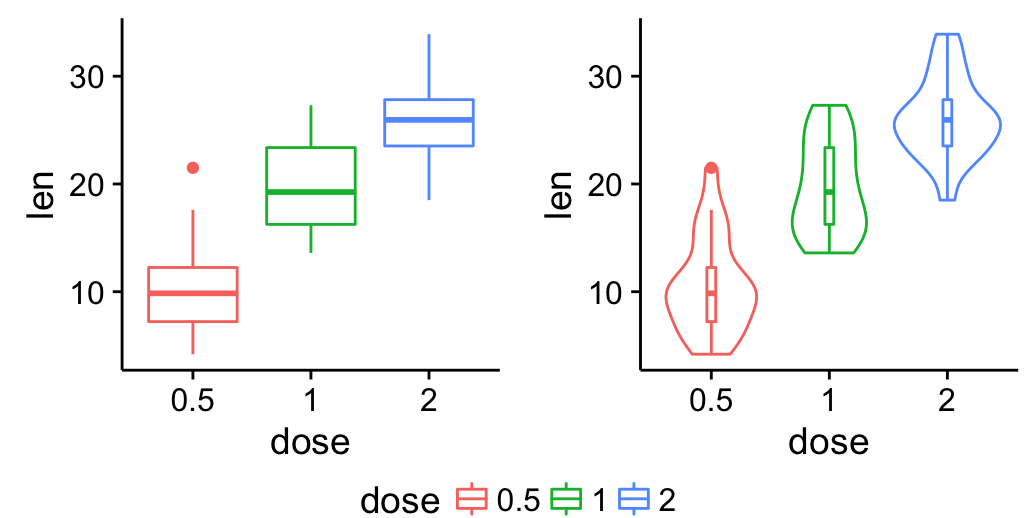
Top-center legend:
- The legend (plot 1) lives in the first row (height = 0.2) spanning two columns
- bp (plot 2) and vp (plot 3) live in the second row (height = 2.5)
grid.arrange(legend, bp, vp, ncol=2, nrow = 2,
layout_matrix = rbind(c(1,1), c(2,3)),
widths = c(2.7, 2.7), heights = c(0.2, 2.5))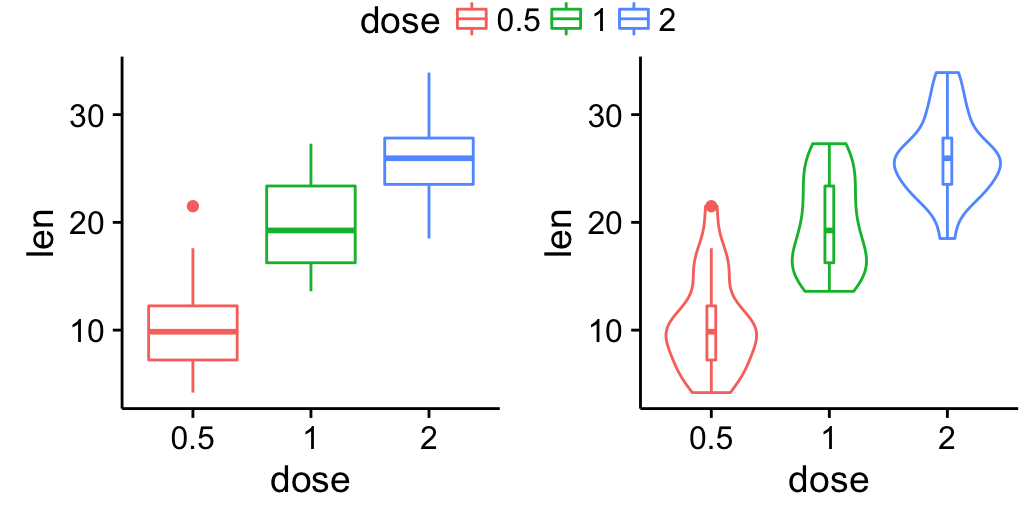
Scatter plot with marginal density plots
Step 1/3. Create some data :
set.seed(1234)
x <- c(rnorm(500, mean = -1), rnorm(500, mean = 1.5))
y <- c(rnorm(500, mean = 1), rnorm(500, mean = 1.7))
group <- as.factor(rep(c(1,2), each=500))
df2 <- data.frame(x, y, group)
head(df2)## x y group
## 1 -2.20706575 -0.2053334 1
## 2 -0.72257076 1.3014667 1
## 3 0.08444118 -0.5391452 1
## 4 -3.34569770 1.6353707 1
## 5 -0.57087531 1.7029518 1
## 6 -0.49394411 -0.9058829 1Step 2/3. Create the plots :
# Scatter plot of x and y variables and color by groups
scatterPlot <- ggplot(df2,aes(x, y, color=group)) +
geom_point() +
scale_color_manual(values = c('#999999','#E69F00')) +
theme(legend.position=c(0,1), legend.justification=c(0,1))
# Marginal density plot of x (top panel)
xdensity <- ggplot(df2, aes(x, fill=group)) +
geom_density(alpha=.5) +
scale_fill_manual(values = c('#999999','#E69F00')) +
theme(legend.position = "none")
# Marginal density plot of y (right panel)
ydensity <- ggplot(df2, aes(y, fill=group)) +
geom_density(alpha=.5) +
scale_fill_manual(values = c('#999999','#E69F00')) +
theme(legend.position = "none")Create a blank placeholder plot :
blankPlot <- ggplot()+geom_blank(aes(1,1))+
theme(
plot.background = element_blank(),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
panel.border = element_blank(),
panel.background = element_blank(),
axis.title.x = element_blank(),
axis.title.y = element_blank(),
axis.text.x = element_blank(),
axis.text.y = element_blank(),
axis.ticks = element_blank(),
axis.line = element_blank()
)Step 3/3. Put the plots together:
Arrange ggplot2 with adapted height and width for each row and column :
library("gridExtra")
grid.arrange(xdensity, blankPlot, scatterPlot, ydensity,
ncol=2, nrow=2, widths=c(4, 1.4), heights=c(1.4, 4))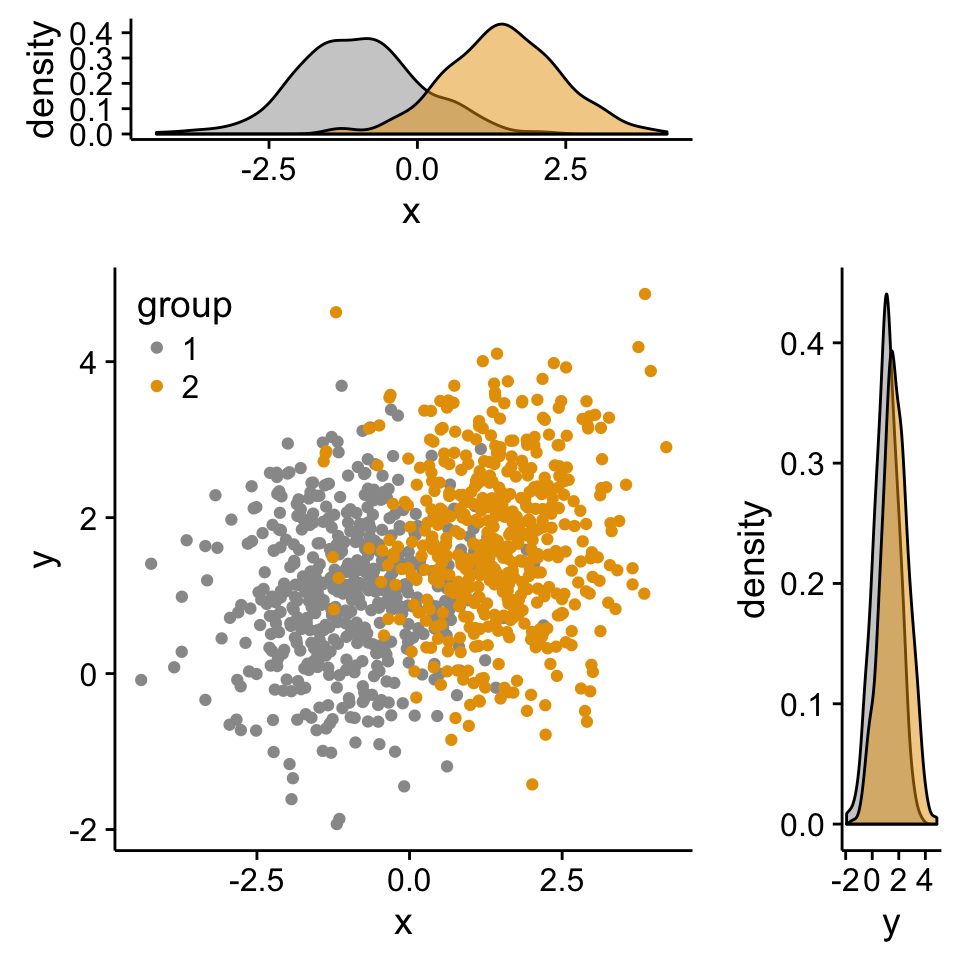
Create a complex layout using the function viewport()
The different steps are :
- Create plots : p1, p2, p3, .
- Move to a new page on a grid device using the function grid.newpage()
- Create a layout 2X2 - number of columns = 2; number of rows = 2
- Define a grid viewport : a rectangular region on a graphics device
- Print a plot into the viewport
# Move to a new page
grid.newpage()
# Create layout : nrow = 2, ncol = 2
pushViewport(viewport(layout = grid.layout(2, 2)))
# A helper function to define a region on the layout
define_region <- function(row, col){
viewport(layout.pos.row = row, layout.pos.col = col)
}
# Arrange the plots
print(scatterPlot, vp=define_region(1, 1:2))
print(xdensity, vp = define_region(2, 1))
print(ydensity, vp = define_region(2, 2))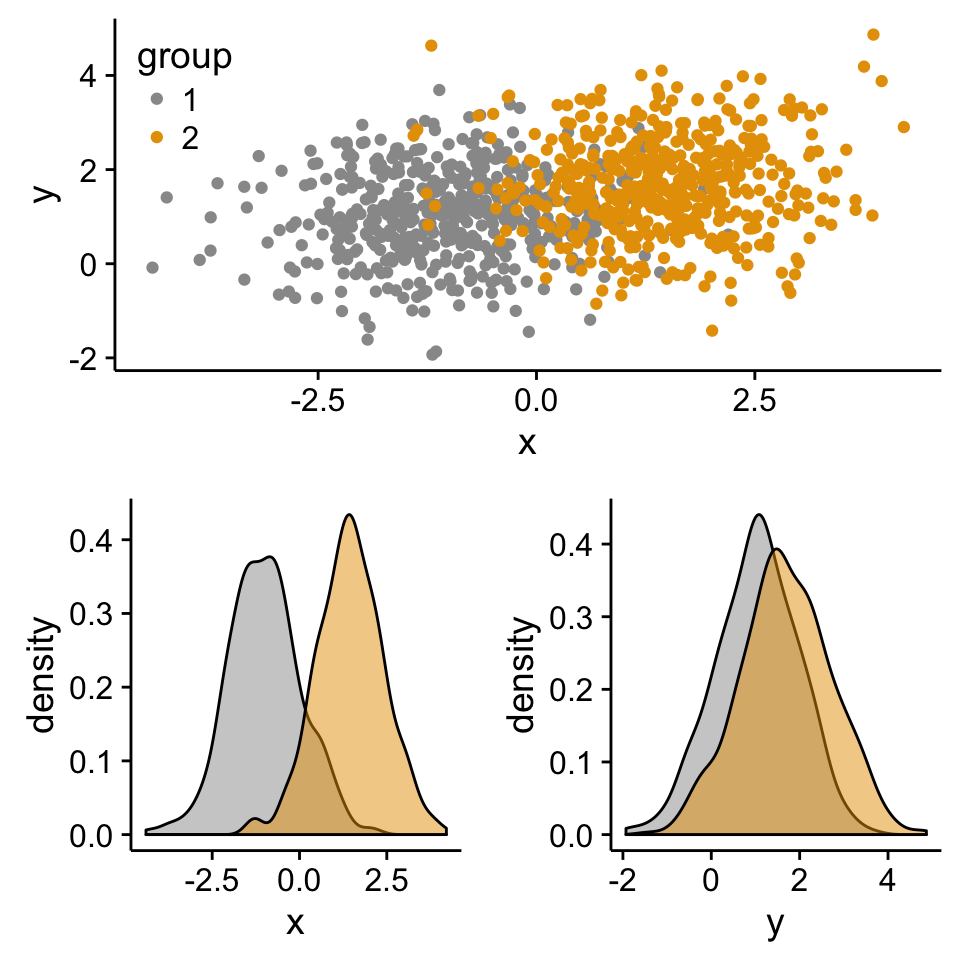
ggExtra: Add marginal distributions plots to ggplot2 scatter plots
The package ggExtra is an easy-to-use package developped by Dean Attali, for adding marginal histograms, boxplots or density plots to ggplot2 scatter plots.
The package can be installed and used as follow:
# Install
install.packages("ggExtra")# Load
library("ggExtra")
# Create some data
set.seed(1234)
x <- c(rnorm(500, mean = -1), rnorm(500, mean = 1.5))
y <- c(rnorm(500, mean = 1), rnorm(500, mean = 1.7))
df3 <- data.frame(x, y)
# Scatter plot of x and y variables and color by groups
sp2 <- ggplot(df3,aes(x, y)) + geom_point()
# Marginal density plot
ggMarginal(sp2 + theme_gray())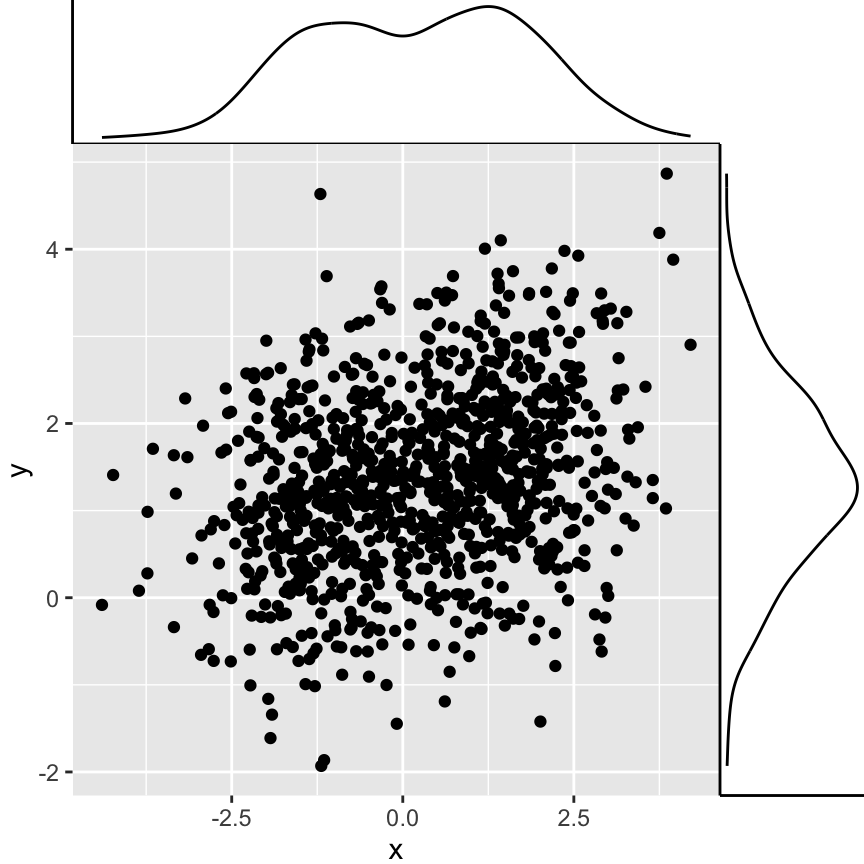
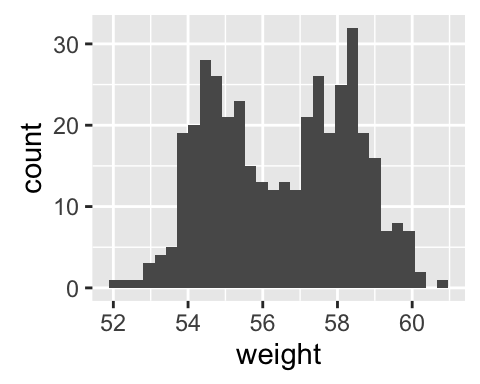
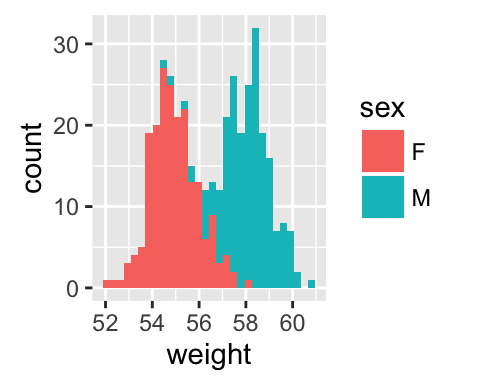
# Marginal histogram plot
ggMarginal(sp2 + theme_gray(), type = "histogram",
fill = "steelblue", col = "darkblue")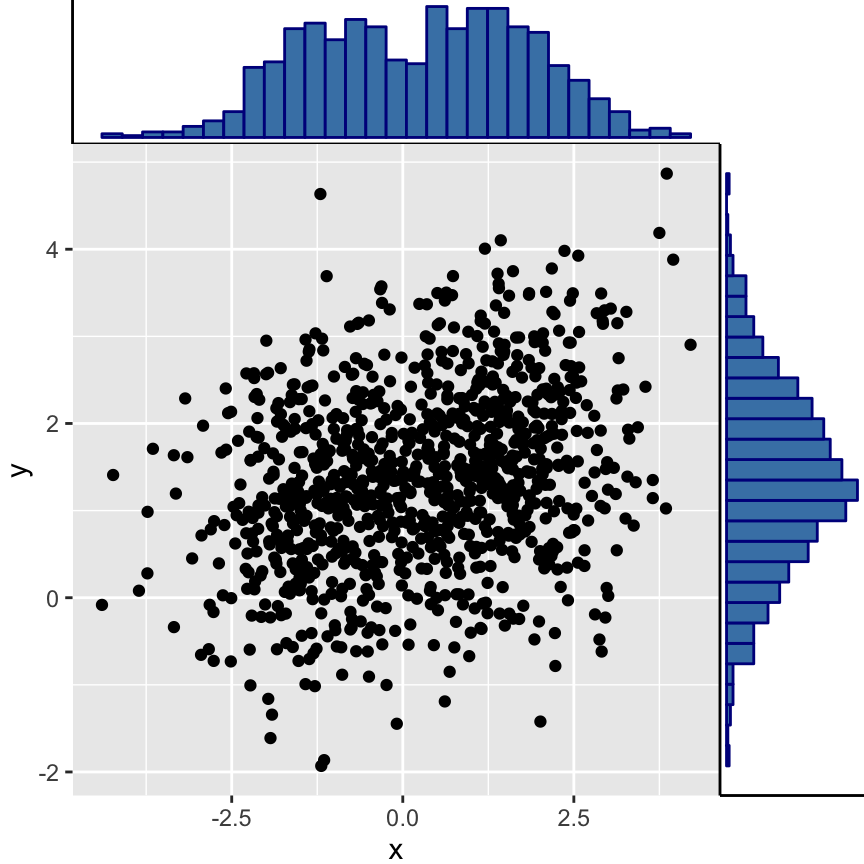
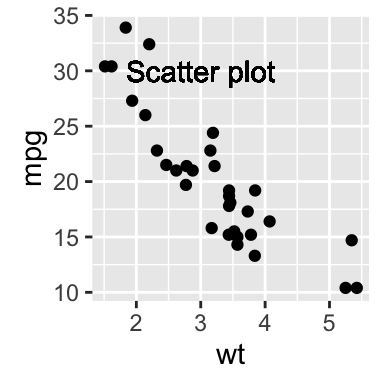
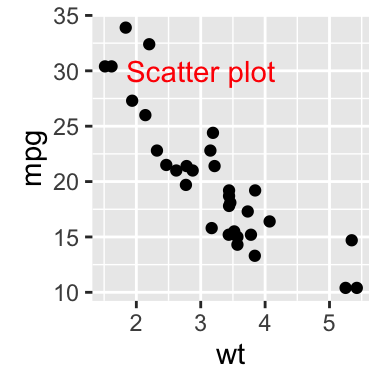
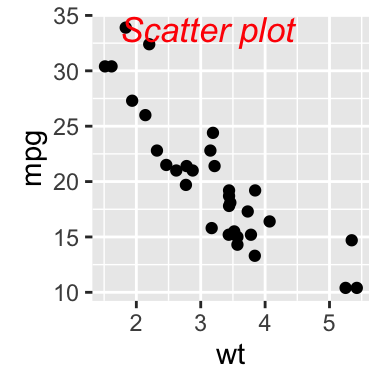
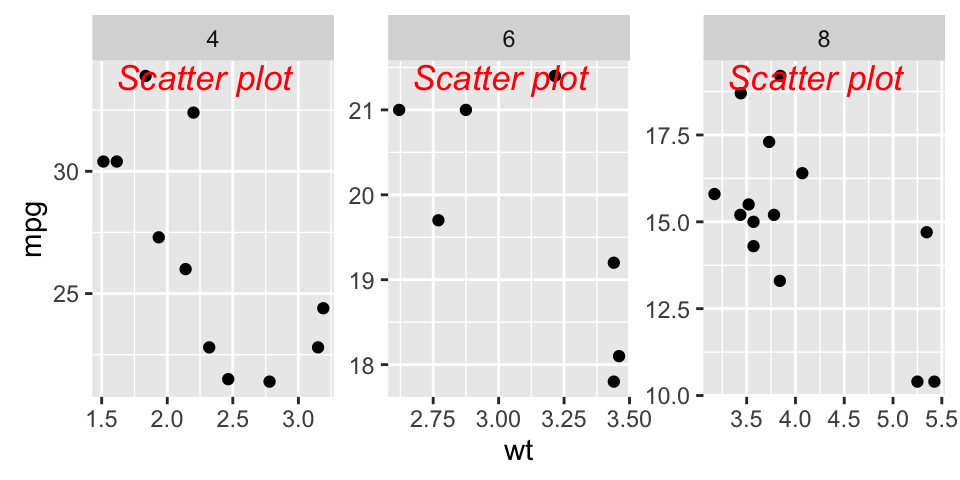
Insert an external graphical element inside a ggplot
The function annotation_custom() [in ggplot2] can be used for adding tables, plots or other grid-based elements. The simplified format is :
annotation_custom(grob, xmin, xmax, ymin, ymax)- grob: the external graphical element to display
- xmin, xmax : x location in data coordinates (horizontal location)
- ymin, ymax : y location in data coordinates (vertical location)
The different steps are :
- Create a scatter plot of y = f(x)
- Add, for example, the box plot of the variables x and y inside the scatter plot using the function annotation_custom()
As the inset box plot overlaps with some points, a transparent background is used for the box plots.
# Create a transparent theme object
transparent_theme <- theme(
axis.title.x = element_blank(),
axis.title.y = element_blank(),
axis.text.x = element_blank(),
axis.text.y = element_blank(),
axis.ticks = element_blank(),
panel.grid = element_blank(),
axis.line = element_blank(),
panel.background = element_rect(fill = "transparent",colour = NA),
plot.background = element_rect(fill = "transparent",colour = NA))Create the graphs :
p1 <- scatterPlot # see previous sections for the scatterPlot
# Box plot of the x variable
p2 <- ggplot(df2, aes(factor(1), x))+
geom_boxplot(width=0.3)+coord_flip()+
transparent_theme
# Box plot of the y variable
p3 <- ggplot(df2, aes(factor(1), y))+
geom_boxplot(width=0.3)+
transparent_theme
# Create the external graphical elements
# called a "grop" in Grid terminology
p2_grob = ggplotGrob(p2)
p3_grob = ggplotGrob(p3)
# Insert p2_grob inside the scatter plot
xmin <- min(x); xmax <- max(x)
ymin <- min(y); ymax <- max(y)
p1 + annotation_custom(grob = p2_grob, xmin = xmin, xmax = xmax,
ymin = ymin-1.5, ymax = ymin+1.5)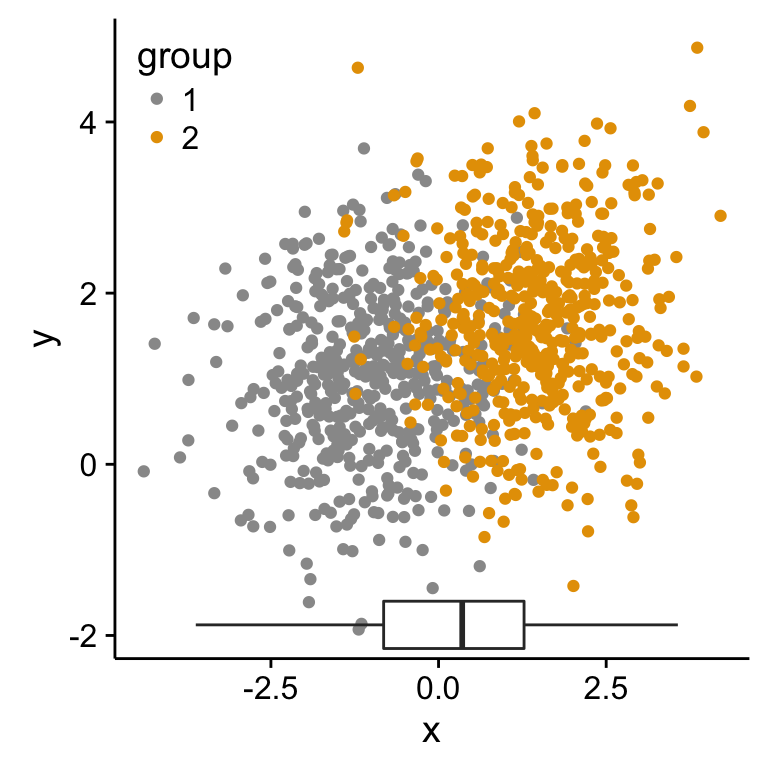
# Insert p3_grob inside the scatter plot
p1 + annotation_custom(grob = p3_grob,
xmin = xmin-1.5, xmax = xmin+1.5,
ymin = ymin, ymax = ymax)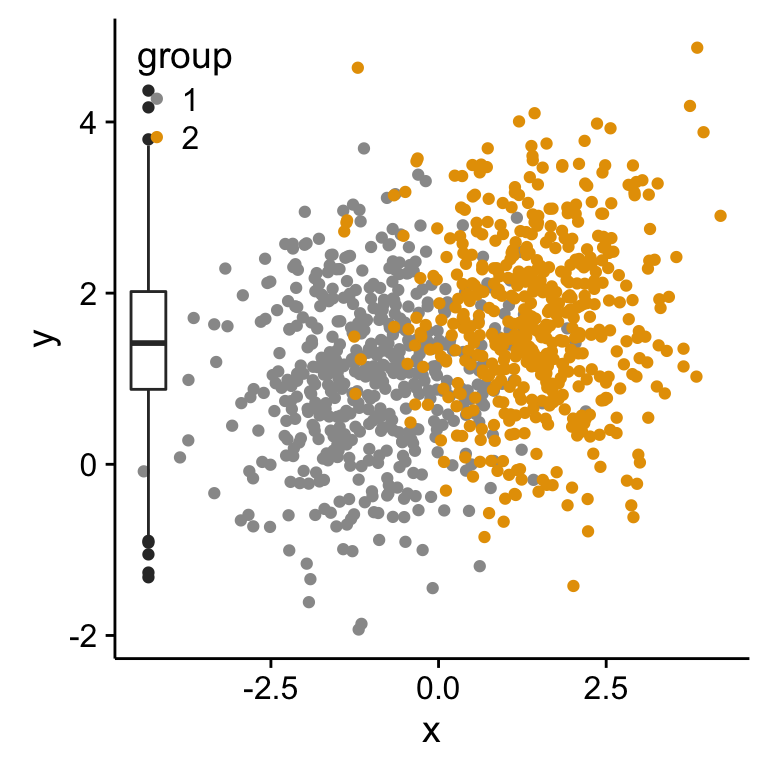
If you have a solution to insert, at the same time, both p2_grob and p3_grob inside the scatter plot, please let me a comment. I got some errors trying to do this
Mix table, text and ggplot2 graphs
The functions below are required :
- tableGrob() [in the package gridExtra] : for adding a data table to a graphic device
- splitTextGrob() [in the package RGraphics] : for adding a text to a graph
Make sure that the package RGraphics is installed.
library(RGraphics)
library(gridExtra)
# Table
p1 <- tableGrob(head(ToothGrowth))
# Text
text <- "ToothGrowth data describes the effect of Vitamin C on tooth growth in Guinea pigs. Three dose levels of Vitamin C (0.5, 1, and 2 mg) with each of two delivery methods [orange juice (OJ) or ascorbic acid (VC)] are used."
p2 <- splitTextGrob(text)
# Box plot
p3 <- ggplot(df, aes(x=dose, y=len)) + geom_boxplot()
# Arrange the plots on the same page
grid.arrange(p1, p2, p3, ncol=1)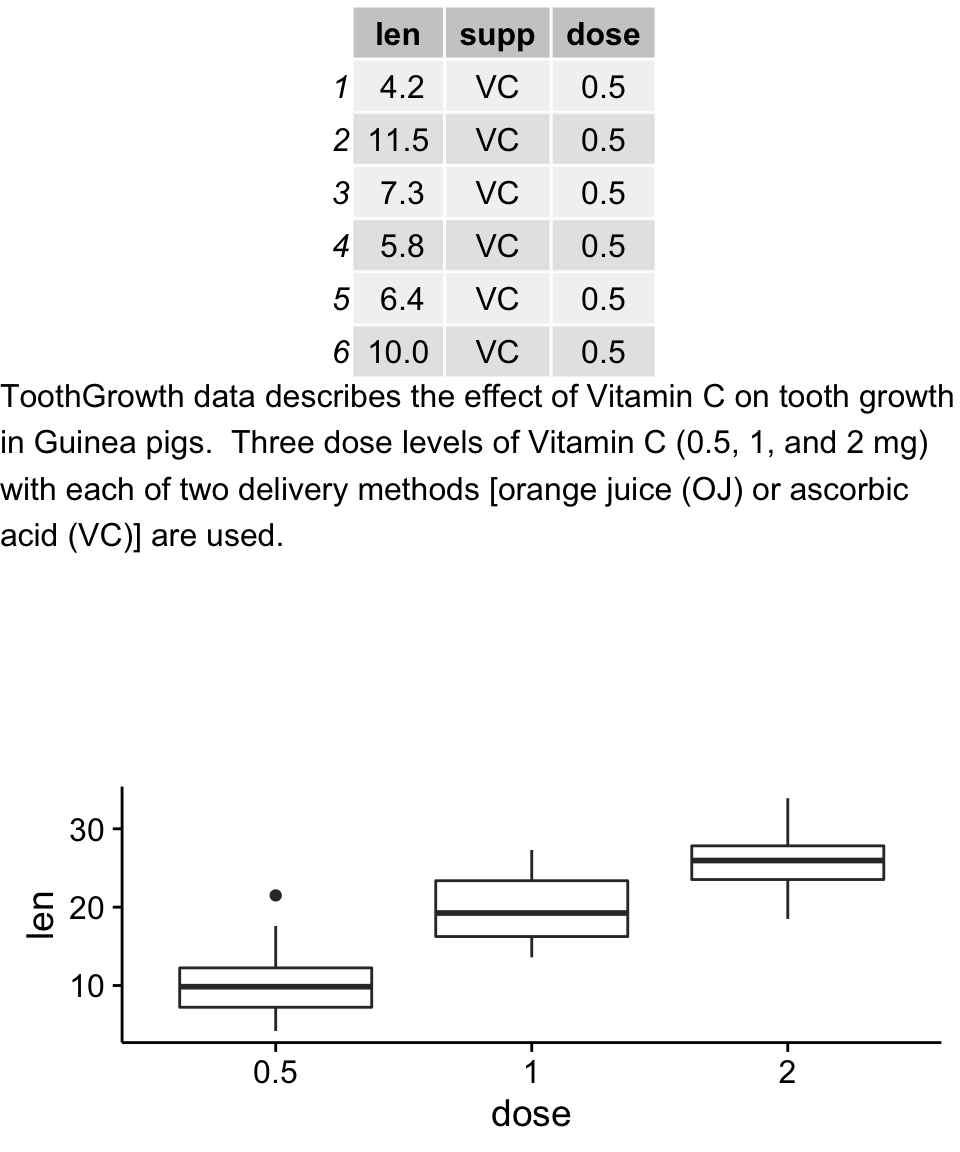
Infos
This analysis has been performed using R software (ver. 3.2.1) and ggplot2 (ver. 1.0.1)