R functions

As you may know, The R function cor() can be used to compute a correlation matrix. A simplified format of the function is :

cor(x, method = c("pearson", "kendall", "spearman"))

If your data contain missing values, use the following R code to handle missing values by case-wise deletion.

cor(x, method = "pearson", use = "complete.obs")

Import your data into R

1. Prepare your data as specified here: Best practices for preparing your data set for R

2. Save your data in an external .txt tab or .csv files

3. Import your data into R as follow:

# If .txt tab file, use this
my_data <- read.delim(file.choose())

# Or, if .csv file, use this
my_data <- read.csv(file.choose())

Here, we’ll use a data derived from the built-in R data set mtcars as an example:

# Load data
data("mtcars")
my_data <- mtcars[, c(1,3,4,5,6,7)]
# print the first 6 rows
head(my_data, 6)

                   mpg disp  hp drat    wt  qsec
Mazda RX4         21.0  160 110 3.90 2.620 16.46
Mazda RX4 Wag     21.0  160 110 3.90 2.875 17.02
Datsun 710        22.8  108  93 3.85 2.320 18.61
Hornet 4 Drive    21.4  258 110 3.08 3.215 19.44
Hornet Sportabout 18.7  360 175 3.15 3.440 17.02
Valiant           18.1  225 105 2.76 3.460 20.22

Compute correlation matrix

res <- cor(my_data)
round(res, 2)

       mpg  disp    hp  drat    wt  qsec
mpg   1.00 -0.85 -0.78  0.68 -0.87  0.42
disp -0.85  1.00  0.79 -0.71  0.89 -0.43
hp   -0.78  0.79  1.00 -0.45  0.66 -0.71
drat  0.68 -0.71 -0.45  1.00 -0.71  0.09
wt   -0.87  0.89  0.66 -0.71  1.00 -0.17
qsec  0.42 -0.43 -0.71  0.09 -0.17  1.00

In the table above correlations coefficients between the possible pairs of variables are shown.

Note that, if your data contain missing values, use the following R code to handle missing values by case-wise deletion.

cor(my_data, use = "complete.obs")

Unfortunately, the function cor() returns only the correlation coefficients between variables. In the next section, we will use Hmisc R package to calculate the correlation p-values.

Correlation matrix with significance levels (p-value)

The function rcorr() [in Hmisc package] can be used to compute the significance levels for pearson and spearman correlations. It returns both the correlation coefficients and the p-value of the correlation for all possible pairs of columns in the data table.

• Simplified format:

rcorr(x, type = c("pearson","spearman"))

x should be a matrix. The correlation type can be either pearson or spearman.

• Install Hmisc package:

install.packages("Hmisc")

• Use rcorr() function

library("Hmisc")
res2 <- rcorr(as.matrix(my_data))
res2

       mpg  disp    hp  drat    wt  qsec
mpg   1.00 -0.85 -0.78  0.68 -0.87  0.42
disp -0.85  1.00  0.79 -0.71  0.89 -0.43
hp   -0.78  0.79  1.00 -0.45  0.66 -0.71
drat  0.68 -0.71 -0.45  1.00 -0.71  0.09
wt   -0.87  0.89  0.66 -0.71  1.00 -0.17
qsec  0.42 -0.43 -0.71  0.09 -0.17  1.00

n= 32 


P
     mpg    disp   hp     drat   wt     qsec  
mpg         0.0000 0.0000 0.0000 0.0000 0.0171
disp 0.0000        0.0000 0.0000 0.0000 0.0131
hp   0.0000 0.0000        0.0100 0.0000 0.0000
drat 0.0000 0.0000 0.0100        0.0000 0.6196
wt   0.0000 0.0000 0.0000 0.0000        0.3389
qsec 0.0171 0.0131 0.0000 0.6196 0.3389       

The output of the function rcorr() is a list containing the following elements : - r : the correlation matrix - n : the matrix of the number of observations used in analyzing each pair of variables - P : the p-values corresponding to the significance levels of correlations.

If you want to extract the p-values or the correlation coefficients from the output, use this:

# Extract the correlation coefficients
res2$r

# Extract p-values
res2$P

A simple function to format the correlation matrix

This section provides a simple function for formatting a correlation matrix into a table with 4 columns containing :

• Column 1 : row names (variable 1 for the correlation test)
• Column 2 : column names (variable 2 for the correlation test)
• Column 3 : the correlation coefficients
• Column 4 : the p-values of the correlations

The custom function below can be used :

# ++++++++++++++++++++++++++++
# flattenCorrMatrix
# ++++++++++++++++++++++++++++
# cormat : matrix of the correlation coefficients
# pmat : matrix of the correlation p-values
flattenCorrMatrix <- function(cormat, pmat) {
  ut <- upper.tri(cormat)
  data.frame(
    row = rownames(cormat)[row(cormat)[ut]],
    column = rownames(cormat)[col(cormat)[ut]],
    cor  =(cormat)[ut],
    p = pmat[ut]
    )
}

Example of usage :

library(Hmisc)
res2<-rcorr(as.matrix(mtcars[,1:7]))
flattenCorrMatrix(res2$r, res2$P)

    row column         cor            p
1   mpg    cyl -0.85216194 6.112697e-10
2   mpg   disp -0.84755135 9.380354e-10
3   cyl   disp  0.90203285 1.803002e-12
4   mpg     hp -0.77616835 1.787838e-07
5   cyl     hp  0.83244747 3.477856e-09
6  disp     hp  0.79094857 7.142686e-08
7   mpg   drat  0.68117189 1.776241e-05
8   cyl   drat -0.69993812 8.244635e-06
9  disp   drat -0.71021390 5.282028e-06
10   hp   drat -0.44875914 9.988768e-03
11  mpg     wt -0.86765939 1.293956e-10
12  cyl     wt  0.78249580 1.217567e-07
13 disp     wt  0.88797992 1.222311e-11
14   hp     wt  0.65874785 4.145833e-05
15 drat     wt -0.71244061 4.784268e-06
16  mpg   qsec  0.41868404 1.708199e-02
17  cyl   qsec -0.59124213 3.660527e-04
18 disp   qsec -0.43369791 1.314403e-02
19   hp   qsec -0.70822340 5.766250e-06
20 drat   qsec  0.09120482 6.195823e-01
21   wt   qsec -0.17471591 3.388682e-01

Visualize correlation matrix

There are different ways for visualizing a correlation matrix in R software :

• symnum() function
• corrplot() function to plot a correlogram
• scatter plots
• heatmap

symnum(x, cutpoints = c(0.3, 0.6, 0.8, 0.9, 0.95),
       symbols = c("", ".", ",", "+", "*", "B"),
       abbr.colnames = TRUE)

symnum(res, abbr.colnames = FALSE)

     mpg disp hp drat wt qsec
mpg  1                       
disp +   1                   
hp   ,   ,    1              
drat ,   ,    .  1           
wt   +   +    ,  ,    1      
qsec .   .    ,          1   
attr(,"legend")
[1] 0 ' ' 0.3 '.' 0.6 ',' 0.8 '+' 0.9 '*' 0.95 'B' 1

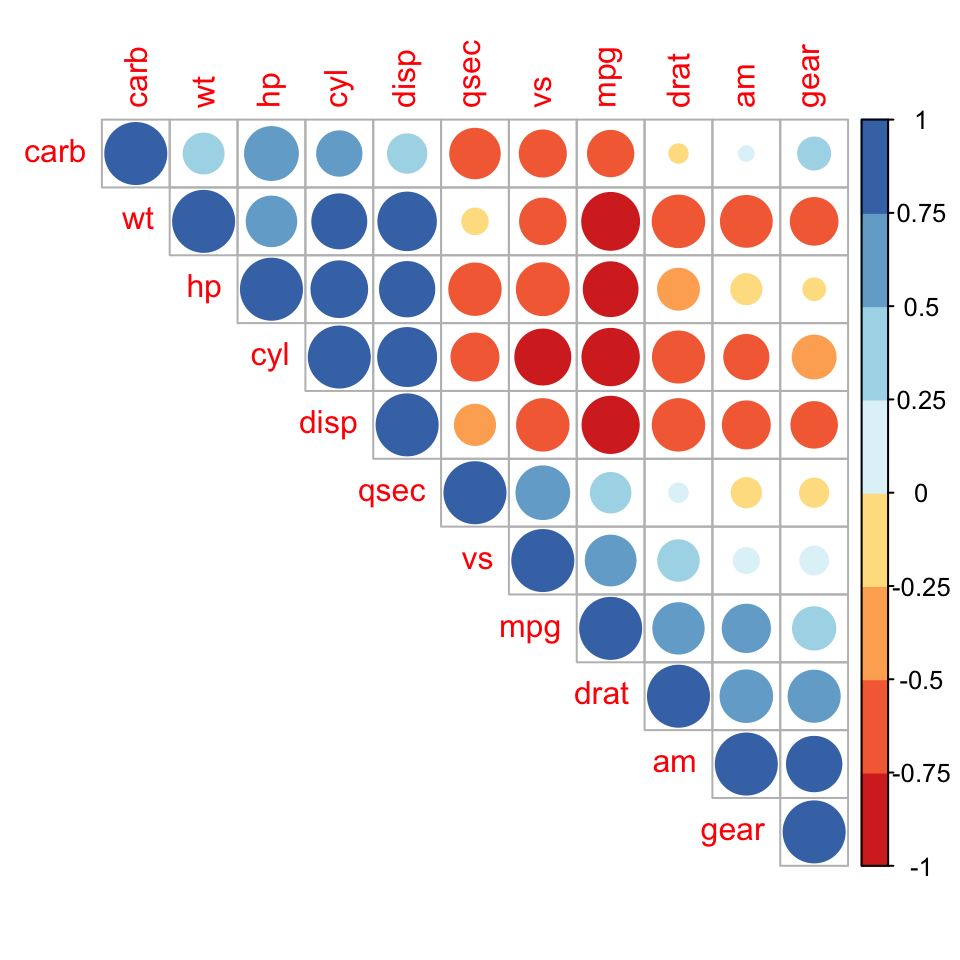
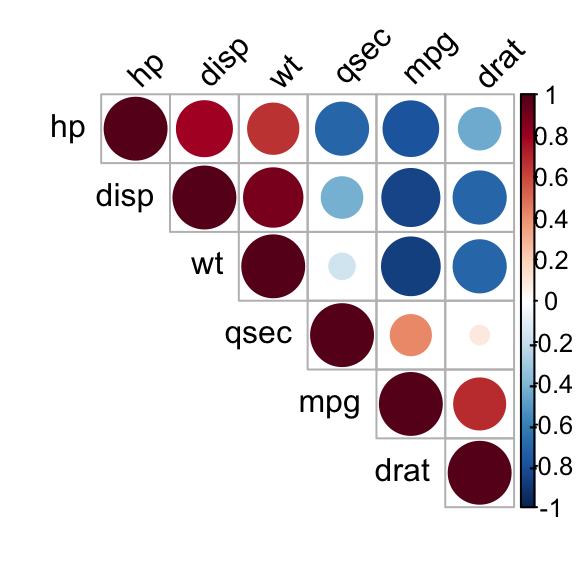
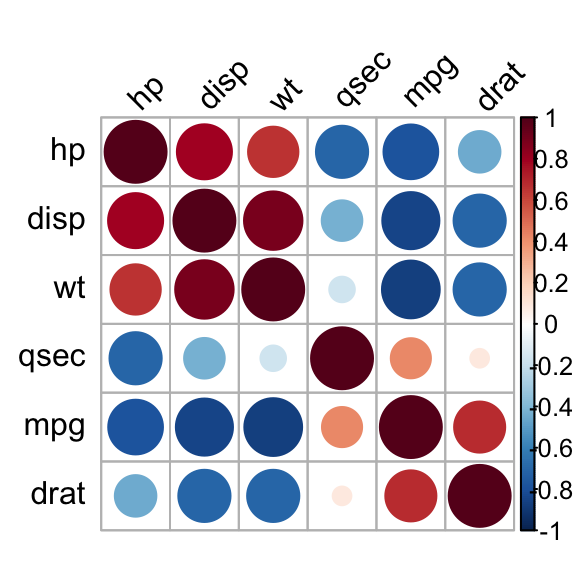
Use corrplot() function: Draw a correlogram

The function corrplot(), in the package of the same name, creates a graphical display of a correlation matrix, highlighting the most correlated variables in a data table.

In this plot, correlation coefficients are colored according to the value. Correlation matrix can be also reordered according to the degree of association between variables.

• Install corrplot:

install.packages("corrplot")

• Use corrplot() to create a correlogram:

The function corrplot() takes the correlation matrix as the first argument. The second argument (type=“upper”) is used to display only the upper triangular of the correlation matrix.

library(corrplot)
corrplot(res, type = "upper", order = "hclust", 
         tl.col = "black", tl.srt = 45)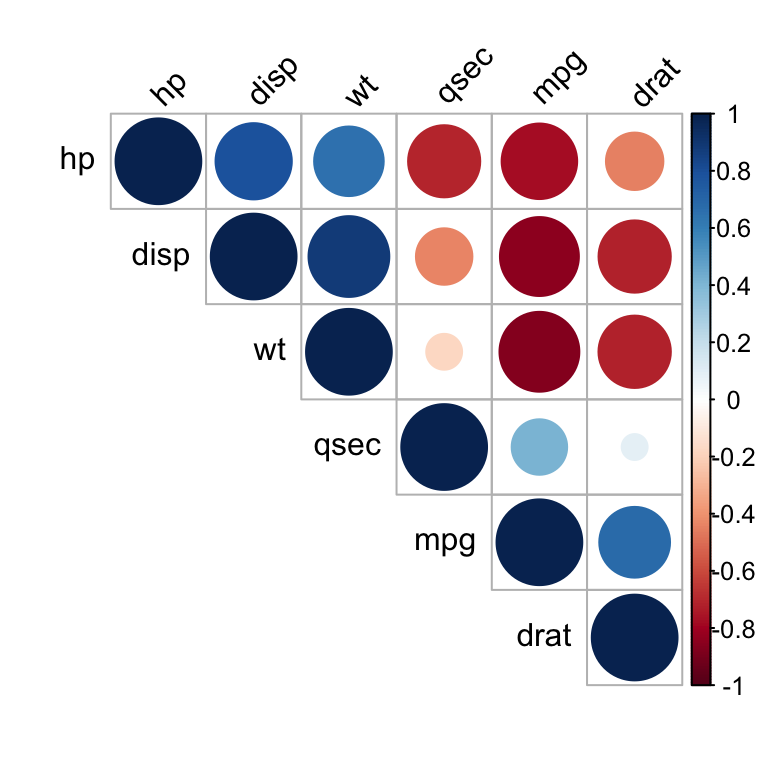

Correlation matrix - R software and statistics

Positive correlations are displayed in blue and negative correlations in red color. Color intensity and the size of the circle are proportional to the correlation coefficients. In the right side of the correlogram, the legend color shows the correlation coefficients and the corresponding colors.

• The correlation matrix is reordered according to the correlation coefficient using “hclust” method.
• tl.col (for text label color) and tl.srt (for text label string rotation) are used to change text colors and rotations.
• Possible values for the argument type are : “upper”, “lower”, “full”

Read more : visualize a correlation matrix using corrplot.

It’s also possible to combine correlogram with the significance test. We’ll use the result res.cor2 generated in the previous section with rcorr() function [in Hmisc package]:

# Insignificant correlation are crossed
corrplot(res2$r, type="upper", order="hclust", 
         p.mat = res2$P, sig.level = 0.01, insig = "blank")
# Insignificant correlations are leaved blank
corrplot(res2$r, type="upper", order="hclust", 
         p.mat = res2$P, sig.level = 0.01, insig = "blank")

Correlation matrix - R software and statistics

In the above plot, correlations with p-value > 0.01 are considered as insignificant. In this case the correlation coefficient values are leaved blank or crosses are added.

Use chart.Correlation(): Draw scatter plots

The function chart.Correlation()[ in the package PerformanceAnalytics], can be used to display a chart of a correlation matrix.

• Install PerformanceAnalytics:

install.packages("PerformanceAnalytics")

• Use chart.Correlation():

library("PerformanceAnalytics")
my_data <- mtcars[, c(1,3,4,5,6,7)]
chart.Correlation(my_data, histogram=TRUE, pch=19)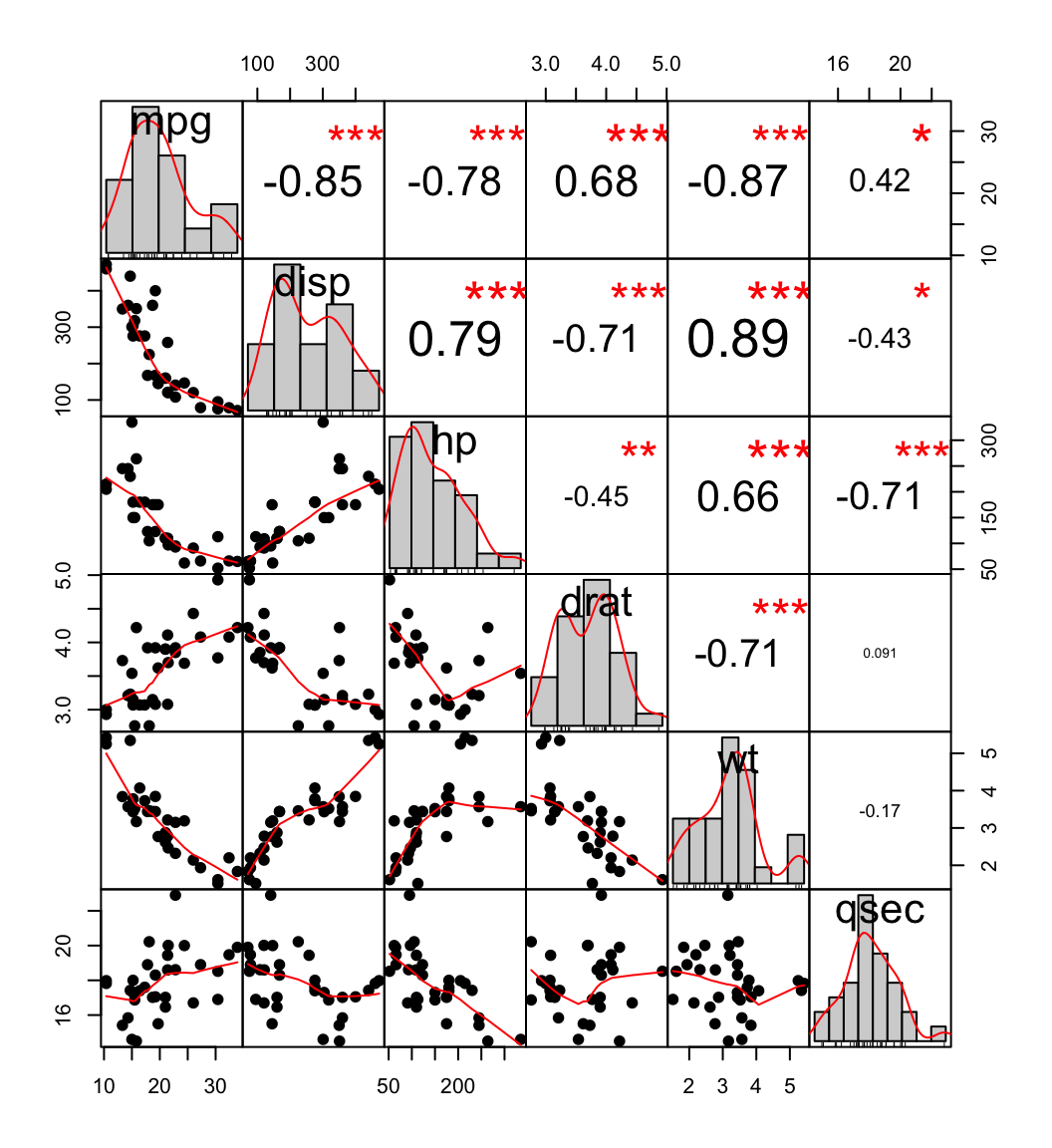

scatter plot, chart

In the above plot:

• The distribution of each variable is shown on the diagonal.
• On the bottom of the diagonal : the bivariate scatter plots with a fitted line are displayed
• On the top of the diagonal : the value of the correlation plus the significance level as stars
• Each significance level is associated to a symbol : p-values(0, 0.001, 0.01, 0.05, 0.1, 1) <=> symbols(“***”, “**”, “*”, “.”, "“)

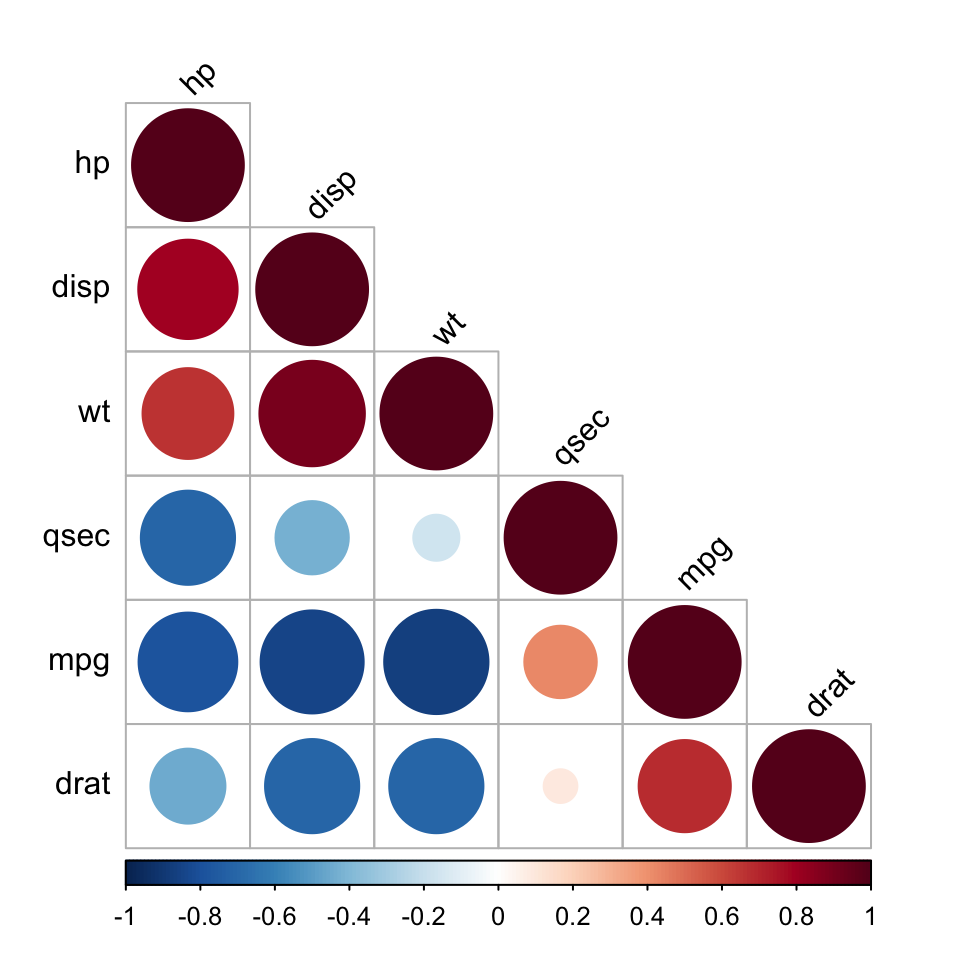
Use heatmap()

# Get some colors
col<- colorRampPalette(c("blue", "white", "red"))(20)
heatmap(x = res, col = col, symm = TRUE)

Heatmap of correlation matrix

• x : the correlation matrix to be plotted
• col : color palettes
• symm : logical indicating if x should be treated symmetrically; can only be true when x is a square matrix.

Install ggpubr R package for data visualization

You can draw R base graphs as described at this link: R base graphs. Here, we’ll use the ggpubr R package for an easy ggplot2-based data visualization

• Install the latest version from GitHub as follow (recommended):

# Install
if(!require(devtools)) install.packages("devtools")
devtools::install_github("kassambara/ggpubr")

• Or, install from CRAN as follow:

install.packages("ggpubr")

R function to compute one-sample Wilcoxon test

To perform one-sample Wilcoxon-test, the R function wilcox.test() can be used as follow:

wilcox.test(x, mu = 0, alternative = "two.sided")

Import your data into R

1. Prepare your data as specified here: Best practices for preparing your data set for R

2. Save your data in an external .txt tab or .csv files

3. Import your data into R as follow:

# If .txt tab file, use this
my_data <- read.delim(file.choose())

# Or, if .csv file, use this
my_data <- read.csv(file.choose())

Here, we’ll use an example data set containing the weight of 10 mice.

We want to know, if the median weight of the mice differs from 25g?

set.seed(1234)
my_data <- data.frame(
  name = paste0(rep("M_", 10), 1:10),
  weight = round(rnorm(10, 20, 2), 1)
)

Check your data

# Print the first 10 rows of the data
head(my_data, 10)

   name weight
1   M_1   17.6
2   M_2   20.6
3   M_3   22.2
4   M_4   15.3
5   M_5   20.9
6   M_6   21.0
7   M_7   18.9
8   M_8   18.9
9   M_9   18.9
10 M_10   18.2

# Statistical summaries of weight
summary(my_data$weight)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  15.30   18.38   18.90   19.25   20.82   22.20 

• Min.: the minimum value
• 1st Qu.: The first quartile. 25% of values are lower than this.
• Median: the median value. Half the values are lower; half are higher.
• 3rd Qu.: the third quartile. 75% of values are higher than this.
• Max.: the maximum value

Visualize your data using box plots

library(ggpubr)
ggboxplot(my_data$weight, 
          ylab = "Weight (g)", xlab = FALSE,
          ggtheme = theme_minimal())

One-Sample Wilcoxon Signed Rank Test in R

Compute one-sample Wilcoxon test

We want to know, if the average weight of the mice differs from 25g (two-tailed test)?

# One-sample wilcoxon test
res <- wilcox.test(my_data$weight, mu = 25)

# Printing the results
res 

    Wilcoxon signed rank test with continuity correction

data:  my_data$weight
V = 0, p-value = 0.005793
alternative hypothesis: true location is not equal to 25

# print only the p-value
res$p.value

[1] 0.005793045

The p-value of the test is 0.005793, which is less than the significance level alpha = 0.05. We can reject the null hypothesis and conclude that the average weight of the mice is significantly different from 25g with a p-value = 0.005793.

wilcox.test(my_data$weight, mu = 25,
              alternative = "less")

wilcox.test(my_data$weight, mu = 25,
              alternative = "greater")

Install ggpubr R package for data visualization

You can draw R base graps as described at this link: R base graphs. Here, we’ll use the ggpubr R package for an easy ggplot2-based data visualization

• Install the latest version from GitHub as follow (recommended):

# Install
if(!require(devtools)) install.packages("devtools")
devtools::install_github("kassambara/ggpubr")

• Or, install from CRAN as follow:

install.packages("ggpubr")

R function to compute one-sample t-test

To perform one-sample t-test, the R function t.test() can be used as follow:

t.test(x, mu = 0, alternative = "two.sided")

Import your data into R

1. Prepare your data as specified here: Best practices for preparing your data set for R

2. Save your data in an external .txt tab or .csv files

3. Import your data into R as follow:

# If .txt tab file, use this
my_data <- read.delim(file.choose())

# Or, if .csv file, use this
my_data <- read.csv(file.choose())

Here, we’ll use an example data set containing the weight of 10 mice.

We want to know, if the average weight of the mice differs from 25g?

set.seed(1234)
my_data <- data.frame(
  name = paste0(rep("M_", 10), 1:10),
  weight = round(rnorm(10, 20, 2), 1)
)

Check your data

# Print the first 10 rows of the data
head(my_data, 10)

   name weight
1   M_1   17.6
2   M_2   20.6
3   M_3   22.2
4   M_4   15.3
5   M_5   20.9
6   M_6   21.0
7   M_7   18.9
8   M_8   18.9
9   M_9   18.9
10 M_10   18.2

# Statistical summaries of weight
summary(my_data$weight)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  15.30   18.38   18.90   19.25   20.82   22.20 

• Min.: the minimum value
• 1st Qu.: The first quartile. 25% of values are lower than this.
• Median: the median value. Half the values are lower; half are higher.
• 3rd Qu.: the third quartile. 75% of values are higher than this.
• Max.: the maximum value

Visualize your data using box plots

library(ggpubr)
ggboxplot(my_data$weight, 
          ylab = "Weight (g)", xlab = FALSE,
          ggtheme = theme_minimal())

One-Sample Student’s T-test in R

Preleminary test to check one-sample t-test assumptions

1. Is this a large sample? - No, because n < 30.
2. Since the sample size is not large enough (less than 30, central limit theorem), we need to check whether the data follow a normal distribution.

How to check the normality?

Read this article: Normality Test in R.

Briefly, it’s possible to use the Shapiro-Wilk normality test and to look at the normality plot.

1. Shapiro-Wilk test:
   • Null hypothesis: the data are normally distributed
   • Alternative hypothesis: the data are not normally distributed

shapiro.test(my_data$weight) # => p-value = 0.6993

From the output, the p-value is greater than the significance level 0.05 implying that the distribution of the data are not significantly different from normal distribtion. In other words, we can assume the normality.

• Visual inspection of the data normality using Q-Q plots (quantile-quantile plots). Q-Q plot draws the correlation between a given sample and the normal distribution.

library("ggpubr")
ggqqplot(my_data$weight, ylab = "Men's weight",
         ggtheme = theme_minimal())

One-Sample Student’s T-test in R

From the normality plots, we conclude that the data may come from normal distributions.

Note that, if the data are not normally distributed, it’s recommended to use the non parametric one-sample Wilcoxon rank test.

Compute one-sample t-test

We want to know, if the average weight of the mice differs from 25g (two-tailed test)?

# One-sample t-test
res <- t.test(my_data$weight, mu = 25)

# Printing the results
res 

    One Sample t-test

data:  my_data$weight
t = -9.0783, df = 9, p-value = 7.953e-06
alternative hypothesis: true mean is not equal to 25
95 percent confidence interval:
 17.8172 20.6828
sample estimates:
mean of x 
    19.25 

t.test(my_data$weight, mu = 25,
              alternative = "less")

t.test(my_data$weight, mu = 25,
              alternative = "greater")

Interpretation of the result

The p-value of the test is 7.95310^{-6}, which is less than the significance level alpha = 0.05. We can conclude that the mean weight of the mice is significantly different from 25g with a p-value = 7.95310^{-6}.

Access to the values returned by t.test() function

The result of t.test() function is a list containing the following components:

The format of the R code to use for getting these values is as follow:

# printing the p-value
res$p.value

[1] 7.953383e-06

# printing the mean
res$estimate

mean of x 
    19.25 

# printing the confidence interval
res$conf.int

[1] 17.8172 20.6828
attr(,"conf.level")
[1] 0.95

Install ggpubr R package for data visualization

You can draw R base graphs as described at this link: R base graphs. Here, we’ll use the ggpubr R package for an easy ggplot2-based data visualization

• Install the latest version from GitHub as follow (recommended):

# Install
if(!require(devtools)) install.packages("devtools")
devtools::install_github("kassambara/ggpubr")

• Or, install from CRAN as follow:

install.packages("ggpubr")

R function to compute unpaired two-samples t-test

To perform two-samples t-test comparing the means of two independent samples (x & y), the R function t.test() can be used as follow:

t.test(x, y, alternative = "two.sided", var.equal = FALSE)

Import your data into R

1. Prepare your data as specified here: Best practices for preparing your data set for R

2. Save your data in an external .txt tab or .csv files

3. Import your data into R as follow:

# If .txt tab file, use this
my_data <- read.delim(file.choose())

# Or, if .csv file, use this
my_data <- read.csv(file.choose())

Here, we’ll use an example data set, which contains the weight of 18 individuals (9 women and 9 men):

# Data in two numeric vectors
women_weight <- c(38.9, 61.2, 73.3, 21.8, 63.4, 64.6, 48.4, 48.8, 48.5)
men_weight <- c(67.8, 60, 63.4, 76, 89.4, 73.3, 67.3, 61.3, 62.4) 
# Create a data frame
my_data <- data.frame( 
                group = rep(c("Woman", "Man"), each = 9),
                weight = c(women_weight,  men_weight)
                )

We want to know, if the average women’s weight differs from the average men’s weight?

Check your data

# Print all data
print(my_data)

   group weight
1  Woman   38.9
2  Woman   61.2
3  Woman   73.3
4  Woman   21.8
5  Woman   63.4
6  Woman   64.6
7  Woman   48.4
8  Woman   48.8
9  Woman   48.5
10   Man   67.8
11   Man   60.0
12   Man   63.4
13   Man   76.0
14   Man   89.4
15   Man   73.3
16   Man   67.3
17   Man   61.3
18   Man   62.4

It’s possible to compute summary statistics (mean and sd) by groups. The dplyr package can be used.

• To install dplyr package, type this:

install.packages("dplyr")

• Compute summary statistics by groups:

library(dplyr)
group_by(my_data, group) %>%
  summarise(
    count = n(),
    mean = mean(weight, na.rm = TRUE),
    sd = sd(weight, na.rm = TRUE)
  )

Source: local data frame [2 x 4]

   group count     mean        sd
  (fctr) (int)    (dbl)     (dbl)
1    Man     9 68.98889  9.375426
2  Woman     9 52.10000 15.596714

Visualize your data using box plots

# Plot weight by group and color by group
library("ggpubr")
ggboxplot(my_data, x = "group", y = "weight", 
          color = "group", palette = c("#00AFBB", "#E7B800"),
        ylab = "Weight", xlab = "Groups")

Unpaired Two-Samples Student’s T-test in R

Preleminary test to check independent t-test assumptions

Assumption 1: Are the two samples independents?

Yes, since the samples from men and women are not related.

Assumtion 2: Are the data from each of the 2 groups follow a normal distribution?

Use Shapiro-Wilk normality test as described at: Normality Test in R. - Null hypothesis: the data are normally distributed - Alternative hypothesis: the data are not normally distributed

We’ll use the functions with() and shapiro.test() to compute Shapiro-Wilk test for each group of samples.

# Shapiro-Wilk normality test for Men's weights
with(my_data, shapiro.test(weight[group == "Man"]))# p = 0.1

# Shapiro-Wilk normality test for Women's weights
with(my_data, shapiro.test(weight[group == "Woman"])) # p = 0.6

From the output, the two p-values are greater than the significance level 0.05 implying that the distribution of the data are not significantly different from the normal distribution. In other words, we can assume the normality.

Note that, if the data are not normally distributed, it’s recommended to use the non parametric two-samples Wilcoxon rank test.

Assumption 3. Do the two populations have the same variances?

We’ll use F-test to test for homogeneity in variances. This can be performed with the function var.test() as follow:

res.ftest <- var.test(weight ~ group, data = my_data)
res.ftest

    F test to compare two variances

data:  weight by group
F = 0.36134, num df = 8, denom df = 8, p-value = 0.1714
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.08150656 1.60191315
sample estimates:
ratio of variances 
         0.3613398 

The p-value of F-test is p = 0.1713596. It’s greater than the significance level alpha = 0.05. In conclusion, there is no significant difference between the variances of the two sets of data. Therefore, we can use the classic t-test witch assume equality of the two variances.

Compute unpaired two-samples t-test

Question : Is there any significant difference between women and men weights?

1) Compute independent t-test - Method 1: The data are saved in two different numeric vectors.

# Compute t-test
res <- t.test(women_weight, men_weight, var.equal = TRUE)
res

    Two Sample t-test

data:  women_weight and men_weight
t = -2.7842, df = 16, p-value = 0.01327
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -29.748019  -4.029759
sample estimates:
mean of x mean of y 
 52.10000  68.98889 

2) Compute independent t-test - Method 2: The data are saved in a data frame.

# Compute t-test
res <- t.test(weight ~ group, data = my_data, var.equal = TRUE)
res

    Two Sample t-test

data:  weight by group
t = 2.7842, df = 16, p-value = 0.01327
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
  4.029759 29.748019
sample estimates:
  mean in group Man mean in group Woman 
           68.98889            52.10000 

As you can see, the two methods give the same results.

t.test(weight ~ group, data = my_data,
        var.equal = TRUE, alternative = "less")

t.test(weight ~ group, data = my_data,
        var.equal = TRUE, alternative = "greater")

Interpretation of the result

The p-value of the test is 0.01327, which is less than the significance level alpha = 0.05. We can conclude that men’s average weight is significantly different from women’s average weight with a p-value = 0.01327.

Access to the values returned by t.test() function

The result of t.test() function is a list containing the following components:

The format of the R code to use for getting these values is as follow:

# printing the p-value
res$p.value

[1] 0.0132656

# printing the mean
res$estimate

  mean in group Man mean in group Woman 
           68.98889            52.10000 

# printing the confidence interval
res$conf.int

[1]  4.029759 29.748019
attr(,"conf.level")
[1] 0.95

R function to compute Wilcoxon test

To perform two-samples Wilcoxon test comparing the means of two independent samples (x & y), the R function wilcox.test() can be used as follow:

wilcox.test(x, y, alternative = "two.sided")

Import your data into R

1. Prepare your data as specified here: Best practices for preparing your data set for R

2. Save your data in an external .txt tab or .csv files

3. Import your data into R as follow:

# If .txt tab file, use this
my_data <- read.delim(file.choose())

# Or, if .csv file, use this
my_data <- read.csv(file.choose())

Here, we’ll use an example data set, which contains the weight of 18 individuals (9 women and 9 men):

# Data in two numeric vectors
women_weight <- c(38.9, 61.2, 73.3, 21.8, 63.4, 64.6, 48.4, 48.8, 48.5)
men_weight <- c(67.8, 60, 63.4, 76, 89.4, 73.3, 67.3, 61.3, 62.4) 
# Create a data frame
my_data <- data.frame( 
                group = rep(c("Woman", "Man"), each = 9),
                weight = c(women_weight,  men_weight)
                )

We want to know, if the median women’s weight differs from the median men’s weight?

Check your data

print(my_data)

   group weight
1  Woman   38.9
2  Woman   61.2
3  Woman   73.3
4  Woman   21.8
5  Woman   63.4
6  Woman   64.6
7  Woman   48.4
8  Woman   48.8
9  Woman   48.5
10   Man   67.8
11   Man   60.0
12   Man   63.4
13   Man   76.0
14   Man   89.4
15   Man   73.3
16   Man   67.3
17   Man   61.3
18   Man   62.4

It’s possible to compute summary statistics (median and interquartile range (IQR)) by groups. The dplyr package can be used.

• To install dplyr package, type this:

install.packages("dplyr")

• Compute summary statistics by groups:

library(dplyr)
group_by(my_data, group) %>%
  summarise(
    count = n(),
    median = median(weight, na.rm = TRUE),
    IQR = IQR(weight, na.rm = TRUE)
  )

Source: local data frame [2 x 4]

   group count median   IQR
  (fctr) (int)  (dbl) (dbl)
1    Man     9   67.3  10.9
2  Woman     9   48.8  15.0

Visualize your data using box plots

You can draw R base graphs as described at this link: R base graphs. Here, we’ll use the ggpubr R package for an easy ggplot2-based data visualization

• Install the latest version of ggpubr from GitHub as follow (recommended):

# Install
if(!require(devtools)) install.packages("devtools")
devtools::install_github("kassambara/ggpubr")

• Or, install from CRAN as follow:

install.packages("ggpubr")

• Visualize your data:

# Plot weight by group and color by group
library("ggpubr")
ggboxplot(my_data, x = "group", y = "weight", 
          color = "group", palette = c("#00AFBB", "#E7B800"),
          ylab = "Weight", xlab = "Groups")

Unpaired Two-Samples Wilcoxon Test in R

Compute unpaired two-samples Wilcoxon test

Question : Is there any significant difference between women and men weights?

1) Compute two-samples Wilcoxon test - Method 1: The data are saved in two different numeric vectors.

res <- wilcox.test(women_weight, men_weight)
res

    Wilcoxon rank sum test with continuity correction

data:  women_weight and men_weight
W = 15, p-value = 0.02712
alternative hypothesis: true location shift is not equal to 0

It will give a warning message, saying that “cannot compute exact p-value with tie”. It comes from the assumption of a Wilcoxon test that the responses are continuous. You can suppress this message by adding another argument exact = FALSE, but the result will be the same.

2) Compute two-samples Wilcoxon test - Method 2: The data are saved in a data frame.

res <- wilcox.test(weight ~ group, data = my_data,
                   exact = FALSE)
res

    Wilcoxon rank sum test with continuity correction

data:  weight by group
W = 66, p-value = 0.02712
alternative hypothesis: true location shift is not equal to 0

# Print the p-value only
res$p.value

[1] 0.02711657

As you can see, the two methods give the same results.

The p-value of the test is 0.02712, which is less than the significance level alpha = 0.05. We can conclude that men’s median weight is significantly different from women’s median weight with a p-value = 0.02712.

wilcox.test(weight ~ group, data = my_data, 
        exact = FALSE, alternative = "less")

wilcox.test(weight ~ group, data = my_data,
        exact = FALSE, alternative = "greater")

R function to compute paired t-test

To perform paired samples t-test comparing the means of two paired samples (x & y), the R function t.test() can be used as follow:

t.test(x, y, paired = TRUE, alternative = "two.sided")

Import your data into R

1. Prepare your data as specified here: Best practices for preparing your data set for R

2. Save your data in an external .txt tab or .csv files

3. Import your data into R as follow:

# If .txt tab file, use this
my_data <- read.delim(file.choose())

# Or, if .csv file, use this
my_data <- read.csv(file.choose())

Here, we’ll use an example data set, which contains the weight of 10 mice before and after the treatment.

# Data in two numeric vectors
# ++++++++++++++++++++++++++
# Weight of the mice before treatment
before <-c(200.1, 190.9, 192.7, 213, 241.4, 196.9, 172.2, 185.5, 205.2, 193.7)
# Weight of the mice after treatment
after <-c(392.9, 393.2, 345.1, 393, 434, 427.9, 422, 383.9, 392.3, 352.2)

# Create a data frame
my_data <- data.frame( 
                group = rep(c("before", "after"), each = 10),
                weight = c(before,  after)
                )

We want to know, if there is any significant difference in the mean weights after treatment?

Check your data

# Print all data
print(my_data)

    group weight
1  before  200.1
2  before  190.9
3  before  192.7
4  before  213.0
5  before  241.4
6  before  196.9
7  before  172.2
8  before  185.5
9  before  205.2
10 before  193.7
11  after  392.9
12  after  393.2
13  after  345.1
14  after  393.0
15  after  434.0
16  after  427.9
17  after  422.0
18  after  383.9
19  after  392.3
20  after  352.2

Compute summary statistics (mean and sd) by groups using the dplyr package.

• To install dplyr package, type this:

install.packages("dplyr")

• Compute summary statistics by groups:

library("dplyr")
group_by(my_data, group) %>%
  summarise(
    count = n(),
    mean = mean(weight, na.rm = TRUE),
    sd = sd(weight, na.rm = TRUE)
  )

Source: local data frame [2 x 4]

   group count   mean       sd
  (fctr) (int)  (dbl)    (dbl)
1  after    10 393.65 29.39801
2 before    10 199.16 18.47354

Visualize your data using box plots

To use R base graphs read this: R base graphs. Here, we’ll use the ggpubr R package for an easy ggplot2-based data visualization.

• Install the latest version of ggpubr from GitHub as follow (recommended):

# Install
if(!require(devtools)) install.packages("devtools")
devtools::install_github("kassambara/ggpubr")

• Or, install from CRAN as follow:

install.packages("ggpubr")

• Visualize your data:

# Plot weight by group and color by group
library("ggpubr")
ggboxplot(my_data, x = "group", y = "weight", 
          color = "group", palette = c("#00AFBB", "#E7B800"),
          order = c("before", "after"),
          ylab = "Weight", xlab = "Groups")

Paired Samples T-test in R

Box plots show you the increase, but lose the paired information. You can use the function plot.paired() [in pairedData package] to plot paired data (“before - after” plot).

• Install pairedData package:

install.packages("PairedData")

• Plot paired data:

# Subset weight data before treatment
before <- subset(my_data,  group == "before", weight,
                 drop = TRUE)
# subset weight data after treatment
after <- subset(my_data,  group == "after", weight,
                 drop = TRUE)
# Plot paired data
library(PairedData)
pd <- paired(before, after)
plot(pd, type = "profile") + theme_bw()

Paired Samples T-test in R

Preleminary test to check paired t-test assumptions

Assumption 1: Are the two samples paired?

Yes, since the data have been collected from measuring twice the weight of the same mice.

Assumption 2: Is this a large sample?

No, because n < 30. Since the sample size is not large enough (less than 30), we need to check whether the differences of the pairs follow a normal distribution.

How to check the normality?

Use Shapiro-Wilk normality test as described at: Normality Test in R.

• Null hypothesis: the data are normally distributed
• Alternative hypothesis: the data are not normally distributed

# compute the difference
d <- with(my_data, 
        weight[group == "before"] - weight[group == "after"])

# Shapiro-Wilk normality test for the differences
shapiro.test(d) # => p-value = 0.6141

From the output, the p-value is greater than the significance level 0.05 implying that the distribution of the differences (d) are not significantly different from normal distribution. In other words, we can assume the normality.

Note that, if the data are not normally distributed, it’s recommended to use the non parametric paired two-samples Wilcoxon test.

Compute paired samples t-test

Question : Is there any significant changes in the weights of mice after treatment?

1) Compute paired t-test - Method 1: The data are saved in two different numeric vectors.

# Compute t-test
res <- t.test(before, after, paired = TRUE)
res

    Paired t-test

data:  before and after
t = -20.883, df = 9, p-value = 6.2e-09
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -215.5581 -173.4219
sample estimates:
mean of the differences 
                -194.49 

2) Compute paired t-test - Method 2: The data are saved in a data frame.

# Compute t-test
res <- t.test(weight ~ group, data = my_data, paired = TRUE)
res

    Paired t-test

data:  weight by group
t = 20.883, df = 9, p-value = 6.2e-09
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 173.4219 215.5581
sample estimates:
mean of the differences 
                 194.49 

As you can see, the two methods give the same results.

t.test(weight ~ group, data = my_data, paired = TRUE,
        alternative = "less")

t.test(weight ~ group, data = my_data, paired = TRUE,
       alternative = "greater")

Interpretation of the result

The p-value of the test is 6.210^{-9}, which is less than the significance level alpha = 0.05. We can then reject null hypothesis and conclude that the average weight of the mice before treatment is significantly different from the average weight after treatment with a p-value = 6.210^{-9}.

Access to the values returned by t.test() function

The result of t.test() function is a list containing the following components:

The format of the R code to use for getting these values is as follow:

# printing the p-value
res$p.value

[1] 6.200298e-09

# printing the mean
res$estimate

mean of the differences 
                 194.49 

# printing the confidence interval
res$conf.int

[1] 173.4219 215.5581
attr(,"conf.level")
[1] 0.95

R function

The R function wilcox.test() can be used as follow:

wilcox.test(x, y, paired = TRUE, alternative = "two.sided")

Import your data into R

1. Prepare your data as specified here: Best practices for preparing your data set for R

2. Save your data in an external .txt tab or .csv files

3. Import your data into R as follow:

# If .txt tab file, use this
my_data <- read.delim(file.choose())

# Or, if .csv file, use this
my_data <- read.csv(file.choose())

Here, we’ll use an example data set, which contains the weight of 10 mice before and after the treatment.

# Data in two numeric vectors
# ++++++++++++++++++++++++++
# Weight of the mice before treatment
before <-c(200.1, 190.9, 192.7, 213, 241.4, 196.9, 172.2, 185.5, 205.2, 193.7)
# Weight of the mice after treatment
after <-c(392.9, 393.2, 345.1, 393, 434, 427.9, 422, 383.9, 392.3, 352.2)

# Create a data frame
my_data <- data.frame( 
                group = rep(c("before", "after"), each = 10),
                weight = c(before,  after)
                )

We want to know, if there is any significant difference in the median weights before and after treatment?

Check your data

# Print all data
print(my_data)

    group weight
1  before  200.1
2  before  190.9
3  before  192.7
4  before  213.0
5  before  241.4
6  before  196.9
7  before  172.2
8  before  185.5
9  before  205.2
10 before  193.7
11  after  392.9
12  after  393.2
13  after  345.1
14  after  393.0
15  after  434.0
16  after  427.9
17  after  422.0
18  after  383.9
19  after  392.3
20  after  352.2

Compute summary statistics (median and inter-quartile range (IQR)) by groups using the dplyr package can be used.

• Install dplyr package:

install.packages("dplyr")

• Compute summary statistics by groups:

library("dplyr")
group_by(my_data, group) %>%
  summarise(
    count = n(),
    median = median(weight, na.rm = TRUE),
    IQR = IQR(weight, na.rm = TRUE)
  )

Source: local data frame [2 x 4]

   group count median    IQR
  (fctr) (int)  (dbl)  (dbl)
1  after    10 392.95 28.800
2 before    10 195.30 12.575

Visualize your data using box plots

• To use R base graphs read this: R base graphs. Here, we’ll use the ggpubr R package for an easy ggplot2-based data visualization.

• Install the latest version of ggpubr from GitHub as follow (recommended):

# Install
if(!require(devtools)) install.packages("devtools")
devtools::install_github("kassambara/ggpubr")

• Or, install from CRAN as follow:

install.packages("ggpubr")

• Visualize your data:

# Plot weight by group and color by group
library("ggpubr")
ggboxplot(my_data, x = "group", y = "weight", 
          color = "group", palette = c("#00AFBB", "#E7B800"),
          order = c("before", "after"),
          ylab = "Weight", xlab = "Groups")

Paired Samples Wilcoxon Test in R

Box plots show you the increase, but lose the paired information. You can use the function plot.paired() [in pairedData package] to plot paired data (“before - after” plot).

• Install pairedData package:

install.packages("PairedData")

• Plot paired data:

# Subset weight data before treatment
before <- subset(my_data,  group == "before", weight,
                 drop = TRUE)
# subset weight data after treatment
after <- subset(my_data,  group == "after", weight,
                 drop = TRUE)
# Plot paired data
library(PairedData)
pd <- paired(before, after)
plot(pd, type = "profile") + theme_bw()

Paired Samples Wilcoxon Test in R

Compute paired-sample Wilcoxon test

Question : Is there any significant changes in the weights of mice before after treatment?

1) Compute paired Wilcoxon test - Method 1: The data are saved in two different numeric vectors.

res <- wilcox.test(before, after, paired = TRUE)
res

    Wilcoxon signed rank test

data:  before and after
V = 0, p-value = 0.001953
alternative hypothesis: true location shift is not equal to 0

2) Compute paired Wilcoxon-test - Method 2: The data are saved in a data frame.

# Compute t-test
res <- wilcox.test(weight ~ group, data = my_data, paired = TRUE)
res

    Wilcoxon signed rank test

data:  weight by group
V = 55, p-value = 0.001953
alternative hypothesis: true location shift is not equal to 0

# print only the p-value
res$p.value

[1] 0.001953125

As you can see, the two methods give the same results.

The p-value of the test is 0.001953, which is less than the significance level alpha = 0.05. We can conclude that the median weight of the mice before treatment is significantly different from the median weight after treatment with a p-value = 0.001953.

wilcox.test(weight ~ group, data = my_data, paired = TRUE,
        alternative = "less")

wilcox.test(weight ~ group, data = my_data, paired = TRUE,
       alternative = "greater")

Import your data into R

1. Prepare your data as specified here: Best practices for preparing your data set for R

2. Save your data in an external .txt tab or .csv files

3. Import your data into R as follow:

# If .txt tab file, use this
my_data <- read.delim(file.choose())

# Or, if .csv file, use this
my_data <- read.csv(file.choose())

Here, we’ll use the built-in R data set named PlantGrowth. It contains the weight of plants obtained under a control and two different treatment conditions.

my_data <- PlantGrowth

Check your data

To have an idea of what the data look like, we use the the function sample_n()[in dplyr package]. The sample_n() function randomly picks a few of the observations in the data frame to print out:

# Show a random sample
set.seed(1234)
dplyr::sample_n(my_data, 10)

   weight group
19   4.32  trt1
18   4.89  trt1
29   5.80  trt2
24   5.50  trt2
17   6.03  trt1
1    4.17  ctrl
6    4.61  ctrl
16   3.83  trt1
12   4.17  trt1
15   5.87  trt1

In R terminology, the column “group” is called factor and the different categories (“ctr”, “trt1”, “trt2”) are named factor levels. The levels are ordered alphabetically.

# Show the levels
levels(my_data$group)

[1] "ctrl""trt1""trt2"

If the levels are not automatically in the correct order, re-order them as follow:

my_data$group <- ordered(my_data$group,
                         levels = c("ctrl", "trt1", "trt2"))

It’s possible to compute summary statistics (mean and sd) by groups using the dplyr package.

• Compute summary statistics by groups - count, mean, sd:

library(dplyr)
group_by(my_data, group) %>%
  summarise(
    count = n(),
    mean = mean(weight, na.rm = TRUE),
    sd = sd(weight, na.rm = TRUE)
  )

Source: local data frame [3 x 4]

   group count  mean        sd
  (fctr) (int) (dbl)     (dbl)
1   ctrl    10 5.032 0.5830914
2   trt1    10 4.661 0.7936757
3   trt2    10 5.526 0.4425733

Visualize your data

• To use R base graphs read this: R base graphs. Here, we’ll use the ggpubr R package for an easy ggplot2-based data visualization.

• Install the latest version of ggpubr from GitHub as follow (recommended):

# Install
if(!require(devtools)) install.packages("devtools")
devtools::install_github("kassambara/ggpubr")

• Or, install from CRAN as follow:

install.packages("ggpubr")

• Visualize your data with ggpubr:

# Box plots
# ++++++++++++++++++++
# Plot weight by group and color by group
library("ggpubr")
ggboxplot(my_data, x = "group", y = "weight", 
          color = "group", palette = c("#00AFBB", "#E7B800", "#FC4E07"),
          order = c("ctrl", "trt1", "trt2"),
          ylab = "Weight", xlab = "Treatment")

One-way ANOVA Test in R

# Mean plots
# ++++++++++++++++++++
# Plot weight by group
# Add error bars: mean_se
# (other values include: mean_sd, mean_ci, median_iqr, ....)
library("ggpubr")
ggline(my_data, x = "group", y = "weight", 
       add = c("mean_se", "jitter"), 
       order = c("ctrl", "trt1", "trt2"),
       ylab = "Weight", xlab = "Treatment")

One-way ANOVA Test in R

If you still want to use R base graphs, type the following scripts:

# Box plot
boxplot(weight ~ group, data = my_data,
        xlab = "Treatment", ylab = "Weight",
        frame = FALSE, col = c("#00AFBB", "#E7B800", "#FC4E07"))

# plotmeans
library("gplots")
plotmeans(weight ~ group, data = my_data, frame = FALSE,
          xlab = "Treatment", ylab = "Weight",
          main="Mean Plot with 95% CI") 

Compute one-way ANOVA test

We want to know if there is any significant difference between the average weights of plants in the 3 experimental conditions.

The R function aov() can be used to answer to this question. The function summary.aov() is used to summarize the analysis of variance model.

# Compute the analysis of variance
res.aov <- aov(weight ~ group, data = my_data)
# Summary of the analysis
summary(res.aov)

            Df Sum Sq Mean Sq F value Pr(>F)  
group        2  3.766  1.8832   4.846 0.0159 *
Residuals   27 10.492  0.3886                 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The output includes the columns F value and Pr(>F) corresponding to the p-value of the test.

Interpret the result of one-way ANOVA tests

As the p-value is less than the significance level 0.05, we can conclude that there are significant differences between the groups highlighted with “*" in the model summary.

Multiple pairwise-comparison between the means of groups

In one-way ANOVA test, a significant p-value indicates that some of the group means are different, but we don’t know which pairs of groups are different.

It’s possible to perform multiple pairwise-comparison, to determine if the mean difference between specific pairs of group are statistically significant.

TukeyHSD(res.aov)

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = weight ~ group, data = my_data)

$group
            diff        lwr       upr     p adj
trt1-ctrl -0.371 -1.0622161 0.3202161 0.3908711
trt2-ctrl  0.494 -0.1972161 1.1852161 0.1979960
trt2-trt1  0.865  0.1737839 1.5562161 0.0120064

glht(model, lincft)

library(multcomp)
summary(glht(res.aov, linfct = mcp(group = "Tukey")))

     Simultaneous Tests for General Linear Hypotheses

Multiple Comparisons of Means: Tukey Contrasts


Fit: aov(formula = weight ~ group, data = my_data)

Linear Hypotheses:
                 Estimate Std. Error t value Pr(>|t|)  
trt1 - ctrl == 0  -0.3710     0.2788  -1.331    0.391  
trt2 - ctrl == 0   0.4940     0.2788   1.772    0.198  
trt2 - trt1 == 0   0.8650     0.2788   3.103    0.012 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Adjusted p values reported -- single-step method)

pairwise.t.test(my_data$weight, my_data$group,
                 p.adjust.method = "BH")

    Pairwise comparisons using t tests with pooled SD 

data:  my_data$weight and my_data$group 

     ctrl  trt1 
trt1 0.194 -    
trt2 0.132 0.013

P value adjustment method: BH 

Check ANOVA assumptions: test validity?

The ANOVA test assumes that, the data are normally distributed and the variance across groups are homogeneous. We can check that with some diagnostic plots.

Check the homogeneity of variance assumption

The residuals versus fits plot can be used to check the homogeneity of variances.

In the plot below, there is no evident relationships between residuals and fitted values (the mean of each groups), which is good. So, we can assume the homogeneity of variances.

# 1. Homogeneity of variances
plot(res.aov, 1)

One-way ANOVA Test in R

Points 17, 15, 4 are detected as outliers, which can severely affect normality and homogeneity of variance. It can be useful to remove outliers to meet the test assumptions.

It’s also possible to use Bartlett’s test or Levene’s test to check the homogeneity of variances.

We recommend Levene’s test, which is less sensitive to departures from normal distribution. The function leveneTest() [in car package] will be used:

library(car)
leveneTest(weight ~ group, data = my_data)

Levene's Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  2  1.1192 0.3412
      27               

From the output above we can see that the p-value is not less than the significance level of 0.05. This means that there is no evidence to suggest that the variance across groups is statistically significantly different. Therefore, we can assume the homogeneity of variances in the different treatment groups.

oneway.test(weight ~ group, data = my_data)

pairwise.t.test(my_data$weight, my_data$group,
                 p.adjust.method = "BH", pool.sd = FALSE)

Check the normality assumption

Normality plot of residuals. In the plot below, the quantiles of the residuals are plotted against the quantiles of the normal distribution. A 45-degree reference line is also plotted.

The normal probability plot of residuals is used to check the assumption that the residuals are normally distributed. It should approximately follow a straight line.

# 2. Normality
plot(res.aov, 2)

One-way ANOVA Test in R

As all the points fall approximately along this reference line, we can assume normality.

The conclusion above, is supported by the Shapiro-Wilk test on the ANOVA residuals (W = 0.96, p = 0.6) which finds no indication that normality is violated.

# Extract the residuals
aov_residuals <- residuals(object = res.aov )

# Run Shapiro-Wilk test
shapiro.test(x = aov_residuals )

    Shapiro-Wilk normality test

data:  aov_residuals
W = 0.96607, p-value = 0.4379

Non-parametric alternative to one-way ANOVA test

Note that, a non-parametric alternative to one-way ANOVA is Kruskal-Wallisrank sum test, which can be used when ANNOVA assumptions are not met.

kruskal.test(weight ~ group, data = my_data)

    Kruskal-Wallis rank sum test

data:  weight by group
Kruskal-Wallis chi-squared = 7.9882, df = 2, p-value = 0.01842

Import your data into R

1. Prepare your data as specified here: Best practices for preparing your data set for R

2. Save your data in an external .txt tab or .csv files

3. Import your data into R as follow:

# If .txt tab file, use this
my_data <- read.delim(file.choose())

# Or, if .csv file, use this
my_data <- read.csv(file.choose())

Here, we’ll use the built-in R data set named ToothGrowth. It contains data from a study evaluating the effect of vitamin C on tooth growth in Guinea pigs. The experiment has been performed on 60 pigs, where each animal received one of three dose levels of vitamin C (0.5, 1, and 2 mg/day) by one of two delivery methods, (orange juice or ascorbic acid (a form of vitamin C and coded as VC). Tooth length was measured and a sample of the data is shown below.

# Store the data in the variable my_data
my_data <- ToothGrowth

Check your data

To get an idea of what the data look like, we display a random sample of the data using the function sample_n()[in dplyr package]. First, install dplyr if you don’t have it:

install.packages("dplyr")

# Show a random sample
set.seed(1234)
dplyr::sample_n(my_data, 10)

    len supp dose
38  9.4   OJ  0.5
36 10.0   OJ  0.5
37  8.2   OJ  0.5
50 27.3   OJ  1.0
59 29.4   OJ  2.0
1   4.2   VC  0.5
13 15.2   VC  1.0
56 30.9   OJ  2.0
27 26.7   VC  2.0
53 22.4   OJ  2.0

# Check the structure
str(my_data)

'data.frame':   60 obs. of  3 variables:
 $ len : num  4.2 11.5 7.3 5.8 6.4 10 11.2 11.2 5.2 7 ...
 $ supp: Factor w/ 2 levels "OJ","VC": 2 2 2 2 2 2 2 2 2 2 ...
 $ dose: num  0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 ...

From the output above, R considers “dose” as a numeric variable. We’ll convert it as a factor variable (i.e., grouping variable) as follow.

# Convert dose as a factor and recode the levels
# as "D0.5", "D1", "D2"
my_data$dose <- factor(my_data$dose, 
                  levels = c(0.5, 1, 2),
                  labels = c("D0.5", "D1", "D2"))
head(my_data)

   len supp dose
1  4.2   VC D0.5
2 11.5   VC D0.5
3  7.3   VC D0.5
4  5.8   VC D0.5
5  6.4   VC D0.5
6 10.0   VC D0.5

Question: We want to know if tooth length depends on supp and dose.

• Generate frequency tables:

table(my_data$supp, my_data$dose)

    
     D0.5 D1 D2
  OJ   10 10 10
  VC   10 10 10

We have 2X3 design cells with the factors being supp and dose and 10 subjects in each cell. Here, we have a balanced design. In the next sections I’ll describe how to analyse data from balanced designs, since this is the simplest case.

Visualize your data

Box plots and line plots can be used to visualize group differences:

• Box plot to plot the data grouped by the combinations of the levels of the two factors.

• Two-way interaction plot, which plots the mean (or other summary) of the response for two-way combinations of factors, thereby illustrating possible interactions.

• To use R base graphs read this: R base graphs. Here, we’ll use the ggpubr R package for an easy ggplot2-based data visualization.

• Install the latest version of ggpubr from GitHub as follow (recommended):

# Install
if(!require(devtools)) install.packages("devtools")
devtools::install_github("kassambara/ggpubr")

• Or, install from CRAN as follow:

install.packages("ggpubr")

• Visualize your data with ggpubr:

# Box plot with multiple groups
# +++++++++++++++++++++
# Plot tooth length ("len") by groups ("dose")
# Color box plot by a second group: "supp"
library("ggpubr")
ggboxplot(my_data, x = "dose", y = "len", color = "supp",
          palette = c("#00AFBB", "#E7B800"))

Two-Way ANOVA Test in R

# Line plots with multiple groups
# +++++++++++++++++++++++
# Plot tooth length ("len") by groups ("dose")
# Color box plot by a second group: "supp"
# Add error bars: mean_se
# (other values include: mean_sd, mean_ci, median_iqr, ....)
library("ggpubr")
ggline(my_data, x = "dose", y = "len", color = "supp",
       add = c("mean_se", "dotplot"),
       palette = c("#00AFBB", "#E7B800"))

Two-Way ANOVA Test in R

If you still want to use R base graphs, type the following scripts:

# Box plot with two factor variables
boxplot(len ~ supp * dose, data=my_data, frame = FALSE, 
        col = c("#00AFBB", "#E7B800"), ylab="Tooth Length")

# Two-way interaction plot
interaction.plot(x.factor = my_data$dose, trace.factor = my_data$supp, 
                 response = my_data$len, fun = mean, 
                 type = "b", legend = TRUE, 
                 xlab = "Dose", ylab="Tooth Length",
                 pch=c(1,19), col = c("#00AFBB", "#E7B800"))

Arguments used for the function interaction.plot():

Compute two-way ANOVA test

We want to know if tooth length depends on supp and dose.

The R function aov() can be used to answer this question. The function summary.aov() is used to summarize the analysis of variance model.

res.aov2 <- aov(len ~ supp + dose, data = my_data)
summary(res.aov2)

            Df Sum Sq Mean Sq F value   Pr(>F)    
supp         1  205.4   205.4   14.02 0.000429 ***
dose         2 2426.4  1213.2   82.81  < 2e-16 ***
Residuals   56  820.4    14.7                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The output includes the columns F value and Pr(>F) corresponding to the p-value of the test.

From the ANOVA table we can conclude that both supp and dose are statistically significant. dose is the most significant factor variable. These results would lead us to believe that changing delivery methods (supp) or the dose of vitamin C, will impact significantly the mean tooth length.

Not the above fitted model is called additive model. It makes an assumption that the two factor variables are independent. If you think that these two variables might interact to create an synergistic effect, replace the plus symbol (+) by an asterisk (*), as follow.

# Two-way ANOVA with interaction effect
# These two calls are equivalent
res.aov3 <- aov(len ~ supp * dose, data = my_data)
res.aov3 <- aov(len ~ supp + dose + supp:dose, data = my_data)
summary(res.aov3)

            Df Sum Sq Mean Sq F value   Pr(>F)    
supp         1  205.4   205.4  15.572 0.000231 ***
dose         2 2426.4  1213.2  92.000  < 2e-16 ***
supp:dose    2  108.3    54.2   4.107 0.021860 *  
Residuals   54  712.1    13.2                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

It can be seen that the two main effects (supp and dose) are statistically significant, as well as their interaction.

Note that, in the situation where the interaction is not significant you should use the additive model.

Interpret the results

From the ANOVA results, you can conclude the following, based on the p-values and a significance level of 0.05:

• the p-value of supp is 0.000429 (significant), which indicates that the levels of supp are associated with significant different tooth length.
• the p-value of dose is < 2e-16 (significant), which indicates that the levels of dose are associated with significant different tooth length.
• the p-value for the interaction between supp*dose is 0.02 (significant), which indicates that the relationships between dose and tooth length depends on the supp method.

Compute some summary statistics

• Compute mean and SD by groups using dplyr R package:

require("dplyr")
group_by(my_data, supp, dose) %>%
  summarise(
    count = n(),
    mean = mean(len, na.rm = TRUE),
    sd = sd(len, na.rm = TRUE)
  )

Source: local data frame [6 x 5]
Groups: supp [?]

    supp   dose count  mean       sd
  (fctr) (fctr) (int) (dbl)    (dbl)
1     OJ   D0.5    10 13.23 4.459709
2     OJ     D1    10 22.70 3.910953
3     OJ     D2    10 26.06 2.655058
4     VC   D0.5    10  7.98 2.746634
5     VC     D1    10 16.77 2.515309
6     VC     D2    10 26.14 4.797731

• It’s also possible to use the function model.tables() as follow:

model.tables(res.aov3, type="means", se = TRUE)

Multiple pairwise-comparison between the means of groups

In ANOVA test, a significant p-value indicates that some of the group means are different, but we don’t know which pairs of groups are different.

It’s possible to perform multiple pairwise-comparison, to determine if the mean difference between specific pairs of group are statistically significant.

TukeyHSD(res.aov3, which = "dose")

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = len ~ supp + dose + supp:dose, data = my_data)

$dose
          diff       lwr       upr   p adj
D1-D0.5  9.130  6.362488 11.897512 0.0e+00
D2-D0.5 15.495 12.727488 18.262512 0.0e+00
D2-D1    6.365  3.597488  9.132512 2.7e-06

glht(model, lincft)

library(multcomp)
summary(glht(res.aov2, linfct = mcp(dose = "Tukey")))

     Simultaneous Tests for General Linear Hypotheses

Multiple Comparisons of Means: Tukey Contrasts


Fit: aov(formula = len ~ supp + dose, data = my_data)

Linear Hypotheses:
               Estimate Std. Error t value Pr(>|t|)    
D1 - D0.5 == 0    9.130      1.210   7.543   <1e-05 ***
D2 - D0.5 == 0   15.495      1.210  12.802   <1e-05 ***
D2 - D1 == 0      6.365      1.210   5.259   <1e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Adjusted p values reported -- single-step method)

pairwise.t.test(my_data$len, my_data$dose,
                p.adjust.method = "BH")

    Pairwise comparisons using t tests with pooled SD 

data:  my_data$len and my_data$dose 

   D0.5    D1     
D1 1.0e-08 -      
D2 4.4e-16 1.4e-05

P value adjustment method: BH 

Check ANOVA assumptions: test validity?

ANOVA assumes that the data are normally distributed and the variance across groups are homogeneous. We can check that with some diagnostic plots.

Check the homogeneity of variance assumption

The residuals versus fits plot is used to check the homogeneity of variances. In the plot below, there is no evident relationships between residuals and fitted values (the mean of each groups), which is good. So, we can assume the homogeneity of variances.

# 1. Homogeneity of variances
plot(res.aov3, 1)

Two-Way ANOVA Test in R

Points 32 and 23 are detected as outliers, which can severely affect normality and homogeneity of variance. It can be useful to remove outliers to meet the test assumptions.

Use the Levene’s test to check the homogeneity of variances. The function leveneTest() [in car package] will be used:

library(car)
leveneTest(len ~ supp*dose, data = my_data)

Levene's Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  5  1.7086 0.1484
      54               

From the output above we can see that the p-value is not less than the significance level of 0.05. This means that there is no evidence to suggest that the variance across groups is statistically significantly different. Therefore, we can assume the homogeneity of variances in the different treatment groups.

Check the normality assumpttion

Normality plot of the residuals. In the plot below, the quantiles of the residuals are plotted against the quantiles of the normal distribution. A 45-degree reference line is also plotted.

The normal probability plot of residuals is used to verify the assumption that the residuals are normally distributed.

The normal probability plot of the residuals should approximately follow a straight line.

# 2. Normality
plot(res.aov3, 2)

Two-Way ANOVA Test in R

As all the points fall approximately along this reference line, we can assume normality.

The conclusion above, is supported by the Shapiro-Wilk test on the ANOVA residuals (W = 0.98, p = 0.5) which finds no indication that normality is violated.

# Extract the residuals
aov_residuals <- residuals(object = res.aov3)

# Run Shapiro-Wilk test
shapiro.test(x = aov_residuals )

    Shapiro-Wilk normality test

data:  aov_residuals
W = 0.98499, p-value = 0.6694

Import your data into R

1. Prepare your data as specified here: Best practices for preparing your data set for R

2. Save your data in an external .txt tab or .csv files

3. Import your data into R as follow:

# If .txt tab file, use this
my_data <- read.delim(file.choose())

# Or, if .csv file, use this
my_data <- read.csv(file.choose())

Here, we’ll use iris data set:

# Store the data in the variable my_data
my_data <- iris

Check your data

The R code below display a random sample of our data using the function sample_n()[in dplyr package]. First, install dplyr if you don’t have it:

install.packages("dplyr")

# Show a random sample
set.seed(1234)
dplyr::sample_n(my_data, 10)

    Sepal.Length Sepal.Width Petal.Length Petal.Width    Species
94           5.0         2.3          3.3         1.0 versicolor
91           5.5         2.6          4.4         1.2 versicolor
93           5.8         2.6          4.0         1.2 versicolor
127          6.2         2.8          4.8         1.8  virginica
150          5.9         3.0          5.1         1.8  virginica
2            4.9         3.0          1.4         0.2     setosa
34           5.5         4.2          1.4         0.2     setosa
96           5.7         3.0          4.2         1.2 versicolor
74           6.1         2.8          4.7         1.2 versicolor
98           6.2         2.9          4.3         1.3 versicolor

Question: We want to know if there is any significant difference, in sepal and petal length, between the different species.

Compute MANOVA test

The function manova() can be used as follow:

sepl <- iris$Sepal.Length
petl <- iris$Petal.Length

# MANOVA test
res.man <- manova(cbind(Sepal.Length, Petal.Length) ~ Species, data = iris)
summary(res.man)

           Df Pillai approx F num Df den Df    Pr(>F)    
Species     2 0.9885   71.829      4    294 < 2.2e-16 ***
Residuals 147                                            
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# Look to see which differ
summary.aov(res.man)

 Response Sepal.Length :
             Df Sum Sq Mean Sq F value    Pr(>F)    
Species       2 63.212  31.606  119.26 < 2.2e-16 ***
Residuals   147 38.956   0.265                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

 Response Petal.Length :
             Df Sum Sq Mean Sq F value    Pr(>F)    
Species       2 437.10 218.551  1180.2 < 2.2e-16 ***
Residuals   147  27.22   0.185                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

From the output above, it can be seen that the two variables are highly significantly different among Species.

Import your data into R

1. Prepare your data as specified here: Best practices for preparing your data set for R

2. Save your data in an external .txt tab or .csv files

3. Import your data into R as follow:

# If .txt tab file, use this
my_data <- read.delim(file.choose())

# Or, if .csv file, use this
my_data <- read.csv(file.choose())

Here, we’ll use the built-in R data set named PlantGrowth. It contains the weight of plants obtained under a control and two different treatment conditions.

my_data <- PlantGrowth

Check your data

# print the head of the file
head(my_data)

  weight group
1   4.17  ctrl
2   5.58  ctrl
3   5.18  ctrl
4   6.11  ctrl
5   4.50  ctrl
6   4.61  ctrl

In R terminology, the column “group” is called factor and the different categories (“ctr”, “trt1”, “trt2”) are named factor levels. The levels are ordered alphabetically.

# Show the group levels
levels(my_data$group)

[1] "ctrl""trt1""trt2"

If the levels are not automatically in the correct order, re-order them as follow:

my_data$group <- ordered(my_data$group,
                         levels = c("ctrl", "trt1", "trt2"))

It’s possible to compute summary statistics by groups. The dplyr package can be used.

• To install dplyr package, type this:

install.packages("dplyr")

• Compute summary statistics by groups:

library(dplyr)
group_by(my_data, group) %>%
  summarise(
    count = n(),
    mean = mean(weight, na.rm = TRUE),
    sd = sd(weight, na.rm = TRUE),
    median = median(weight, na.rm = TRUE),
    IQR = IQR(weight, na.rm = TRUE)
  )

Source: local data frame [3 x 6]

   group count  mean        sd median    IQR
  (fctr) (int) (dbl)     (dbl)  (dbl)  (dbl)
1   ctrl    10 5.032 0.5830914  5.155 0.7425
2   trt1    10 4.661 0.7936757  4.550 0.6625
3   trt2    10 5.526 0.4425733  5.435 0.4675

Visualize the data using box plots

• To use R base graphs read this: R base graphs. Here, we’ll use the ggpubr R package for an easy ggplot2-based data visualization.

• Install the latest version of ggpubr from GitHub as follow (recommended):

# Install
if(!require(devtools)) install.packages("devtools")
devtools::install_github("kassambara/ggpubr")

• Or, install from CRAN as follow:

install.packages("ggpubr")

• Visualize your data with ggpubr:

# Box plots
# ++++++++++++++++++++
# Plot weight by group and color by group
library("ggpubr")
ggboxplot(my_data, x = "group", y = "weight", 
          color = "group", palette = c("#00AFBB", "#E7B800", "#FC4E07"),
          order = c("ctrl", "trt1", "trt2"),
          ylab = "Weight", xlab = "Treatment")

Kruskal-Wallis Test in R

# Mean plots
# ++++++++++++++++++++
# Plot weight by group
# Add error bars: mean_se
# (other values include: mean_sd, mean_ci, median_iqr, ....)
library("ggpubr")
ggline(my_data, x = "group", y = "weight", 
       add = c("mean_se", "jitter"), 
       order = c("ctrl", "trt1", "trt2"),
       ylab = "Weight", xlab = "Treatment")

Kruskal-Wallis Test in R

Compute Kruskal-Wallis test

We want to know if there is any significant difference between the average weights of plants in the 3 experimental conditions.

The test can be performed using the function kruskal.test() as follow:

kruskal.test(weight ~ group, data = my_data)

    Kruskal-Wallis rank sum test

data:  weight by group
Kruskal-Wallis chi-squared = 7.9882, df = 2, p-value = 0.01842

Interpret

As the p-value is less than the significance level 0.05, we can conclude that there are significant differences between the treatment groups.

Multiple pairwise-comparison between groups

From the output of the Kruskal-Wallis test, we know that there is a significant difference between groups, but we don’t know which pairs of groups are different.

It’s possible to use the function pairwise.wilcox.test() to calculate pairwise comparisons between group levels with corrections for multiple testing.

pairwise.wilcox.test(PlantGrowth$weight, PlantGrowth$group,
                 p.adjust.method = "BH")

    Pairwise comparisons using Wilcoxon rank sum test 

data:  PlantGrowth$weight and PlantGrowth$group 

     ctrl  trt1 
trt1 0.199 -    
trt2 0.095 0.027

P value adjustment method: BH 

The pairwise comparison shows that, only trt1 and trt2 are significantly different (p < 0.05).

2.1 One-sample T-test (parametric)

• What is one-sample t-test?
• Research questions and statistical hypotheses
• Formula of one-sample t-test
• Visualize your data and compute one-sample t-test in R
  • R function to compute one-sample t-test
  • Visualize your data using box plots
  • Preliminary test to check one-sample t-test assumptions
  • Compute one-sample t-test
  • Interpretation of the result

Read more: —>One-Sample T-test.

2.2 One-sample Wilcoxon test (non-parametric)

• What’s one-sample Wilcoxon signed rank test?
• Research questions and statistical hypotheses
• Visualize your data and compute one-sample Wilcoxon test in R
  • R function to compute one-sample Wilcoxon test
  • Visualize your data using box plots
  • Compute one-sample Wilcoxon test

Read more: —>One-Sample Wilcoxon Test (non-parametric).

3.1 Unpaired two samples t-test (parametric)

• What is unpaired two-samples t-test?
• Research questions and statistical hypotheses
• Formula of unpaired two-samples t-test
• Visualize your data and compute unpaired two-samples t-test in R
  • R function to compute unpaired two-samples t-test
  • Visualize your data using box plots
  • Preliminary test to check independent t-test assumptions
  • Compute unpaired two-samples t-test
• Interpretation of the result

Read more: —>Unpaired Two Samples T-test (parametric).

3.2 Unpaired two-samples Wilcoxon test (non-parametric)

• R function to compute Wilcoxon test
• Visualize your data using box plots
• Compute unpaired two-samples Wilcoxon test

Read more: —>Unpaired Two-Samples Wilcoxon Test (non-parametric).

4.1 Paired samples t-test (parametric)

Read more: —>Paired Samples T-test (parametric).

4.2 Paired samples Wilcoxon test (non-parametric)

Read more: —>Paired Samples Wilcoxon Test (non-parametric).

5.1 One-way ANOVA test

An extension of independent two-samples t-test for comparing means in a situation where there are more than two groups.

• What is one-way ANOVA test?
• Assumptions of ANOVA test
• How one-way ANOVA test works?
• Visualize your data and compute one-way ANOVA in R
  • Visualize your data
  • Compute one-way ANOVA test
  • Interpret the result of one-way ANOVA tests
  • Multiple pairwise-comparison between the means of groups
    • Tukey multiple pairewise-comparisons
    • Multiple comparisons using multcomp package
    • Pairwise t-test
  • Check ANOVA assumptions: test validity?
    • Check the homogeneity of variance assumption
    • Relaxing the homogeneity of variance assumption
    • Check the normality assumption
  • Non-parametric alternative to one-way ANOVA test

Read more: —>One-Way ANOVA Test in R.

5.2 Two-Way ANOVA test

• What is two-way ANOVA test?
• Two-way ANOVA test hypotheses
• Assumptions of two-way ANOVA test
• Compute two-way ANOVA test in R: balanced designs
  • Visualize your data
  • Compute two-way ANOVA test
  • Interpret the results
  • Compute some summary statistics
  • Multiple pairwise-comparison between the means of groups
    • Tukey multiple pairewise-comparisons
    • Multiple comparisons using multcomp package
    • Pairwise t-test
  • Check ANOVA assumptions: test validity?
    • Check the homogeneity of variance assumption
  • Check the normality assumption
• Compute two-way ANOVA test in R for unbalanced designs

Read more: —>Two-Way ANOVA Test in R.

Upper triangle of the correlation matrix

rquery.cormat(mydata, type="upper")

$r
     hp disp   wt  qsec   mpg  drat
hp    1 0.79 0.66 -0.71 -0.78 -0.45
disp       1 0.89 -0.43 -0.85 -0.71
wt              1 -0.17 -0.87 -0.71
qsec                  1  0.42 0.091
mpg                         1  0.68
drat                              1

$p
     hp    disp      wt    qsec     mpg    drat
hp    0 7.1e-08 4.1e-05 5.8e-06 1.8e-07    0.01
disp          0 1.2e-11   0.013 9.4e-10 5.3e-06
wt                    0    0.34 1.3e-10 4.8e-06
qsec                          0   0.017    0.62
mpg                                   0 1.8e-05
drat                                          0

$sym
     hp disp wt qsec mpg drat
hp   1  ,    ,  ,    ,   .   
disp    1    +  .    +   ,   
wt           1       +   ,   
qsec            1    .       
mpg                  1   ,   
drat                     1   
attr(,"legend")
[1] 0 ' ' 0.3 '.' 0.6 ',' 0.8 '+' 0.9 '*' 0.95 'B' 1

Full correlation matrix

rquery.cormat(mydata, type="full")

$r
        hp  disp    wt   qsec   mpg   drat
hp    1.00  0.79  0.66 -0.710 -0.78 -0.450
disp  0.79  1.00  0.89 -0.430 -0.85 -0.710
wt    0.66  0.89  1.00 -0.170 -0.87 -0.710
qsec -0.71 -0.43 -0.17  1.000  0.42  0.091
mpg  -0.78 -0.85 -0.87  0.420  1.00  0.680
drat -0.45 -0.71 -0.71  0.091  0.68  1.000

$p
          hp    disp      wt    qsec     mpg    drat
hp   0.0e+00 7.1e-08 4.1e-05 5.8e-06 1.8e-07 1.0e-02
disp 7.1e-08 0.0e+00 1.2e-11 1.3e-02 9.4e-10 5.3e-06
wt   4.1e-05 1.2e-11 0.0e+00 3.4e-01 1.3e-10 4.8e-06
qsec 5.8e-06 1.3e-02 3.4e-01 0.0e+00 1.7e-02 6.2e-01
mpg  1.8e-07 9.4e-10 1.3e-10 1.7e-02 0.0e+00 1.8e-05
drat 1.0e-02 5.3e-06 4.8e-06 6.2e-01 1.8e-05 0.0e+00

$sym
     hp disp wt qsec mpg drat
hp   1                       
disp ,  1                    
wt   ,  +    1               
qsec ,  .       1            
mpg  ,  +    +  .    1       
drat .  ,    ,       ,   1   
attr(,"legend")
[1] 0 ' ' 0.3 '.' 0.6 ',' 0.8 '+' 0.9 '*' 0.95 'B' 1

Change the colors of the correlogram

col<- colorRampPalette(c("blue", "white", "red"))(20)
cormat<-rquery.cormat(mydata, type="full", col=col)

Draw a heatmap

cormat<-rquery.cormat(mydata, graphType="heatmap")

rquery.cormat(mydata, graph=FALSE)

R function

The R function var.test() can be used to compare two variances as follow:

# Method 1
var.test(values ~ groups, data, 
         alternative = "two.sided")

# or Method 2
var.test(x, y, alternative = "two.sided")

Import and check your data into R

To import your data, use the following R code:

# If .txt tab file, use this
my_data <- read.delim(file.choose())

# Or, if .csv file, use this
my_data <- read.csv(file.choose())

Here, we’ll use the built-in R data set named ToothGrowth:

# Store the data in the variable my_data
my_data <- ToothGrowth

To have an idea of what the data look like, we start by displaying a random sample of 10 rows using the function sample_n()[in dplyr package]:

library("dplyr")
sample_n(my_data, 10)

    len supp dose
50 27.3   OJ  1.0
18 14.5   VC  1.0
41 19.7   OJ  1.0
10  7.0   VC  0.5
42 23.3   OJ  1.0
23 33.9   VC  2.0
28 21.5   VC  2.0
9   5.2   VC  0.5
25 26.4   VC  2.0
59 29.4   OJ  2.0

We want to test the equality of variances between the two groups OJ and VC in the column “supp”.

Preleminary test to check F-test assumptions

F-test is very sensitive to departure from the normal assumption. You need to check whether the data is normally distributed before using the F-test.

Shapiro-Wilk test can be used to test whether the normal assumption holds. It’s also possible to use Q-Q plot (quantile-quantile plot) to graphically evaluate the normality of a variable. Q-Q plot draws the correlation between a given sample and the normal distribution.

If there is doubt about normality, the better choice is to use Levene’s test or Fligner-Killeen test, which are less sensitive to departure from normal assumption.

Compute F-test

# F-test
res.ftest <- var.test(len ~ supp, data = my_data)
res.ftest

    F test to compare two variances

data:  len by supp
F = 0.6386, num df = 29, denom df = 29, p-value = 0.2331
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.3039488 1.3416857
sample estimates:
ratio of variances 
         0.6385951 

Interpretation of the result

The p-value of F-test is p = 0.2331433 which is less than the significance level 0.05. In conclusion, there is no significant difference between the two variances.

Access to the values returned by var.test() function

The function var.test() returns a list containing the following components:

The format of the R code to use for getting these values is as follow:

# ratio of variances
res.ftest$estimate

ratio of variances 
         0.6385951 

# p-value of the test
res.ftest$p.value

[1] 0.2331433

R functions: binom.test() & prop.test()

The R functions binom.test() and prop.test() can be used to perform one-proportion test:

• binom.test(): compute exact binomial test. Recommended when sample size is small
• prop.test(): can be used when sample size is large ( N > 30). It uses a normal approximation to binomial

The syntax of the two functions are exactly the same. The simplified format is as follow:

binom.test(x, n, p = 0.5, alternative = "two.sided")

prop.test(x, n, p = NULL, alternative = "two.sided",
          correct = TRUE)

Note that, by default, the function prop.test() used the Yates continuity correction, which is really important if either the expected successes or failures is < 5. If you don’t want the correction, use the additional argument correct = FALSE in prop.test() function. The default value is TRUE. (This option must be set to FALSE to make the test mathematically equivalent to the uncorrected z-test of a proportion.)

Compute one-proportion z-test

We want to know, whether the cancer affects more male than female?

We’ll use the function prop.test()

res <- prop.test(x = 95, n = 160, p = 0.5, 
                 correct = FALSE)

# Printing the results
res 

    1-sample proportions test without continuity correction

data:  95 out of 160, null probability 0.5
X-squared = 5.625, df = 1, p-value = 0.01771
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
 0.5163169 0.6667870
sample estimates:
      p 
0.59375 

prop.test(x = 95, n = 160, p = 0.5, correct = FALSE,
           alternative = "less")

prop.test(x = 95, n = 160, p = 0.5, correct = FALSE,
              alternative = "greater")

Interpretation of the result

The p-value of the test is 0.01771, which is less than the significance level alpha = 0.05. We can conclude that the proportion of male with cancer is significantly different from 0.5 with a p-value = 0.01771.

Access to the values returned by prop.test()

The result of prop.test() function is a list containing the following components:

The format of the R code to use for getting these values is as follow:

# printing the p-value
res$p.value

[1] 0.01770607

# printing the mean
res$estimate

      p 
0.59375 

# printing the confidence interval
res$conf.int

[1] 0.5163169 0.6667870
attr(,"conf.level")
[1] 0.95