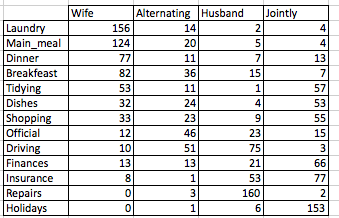
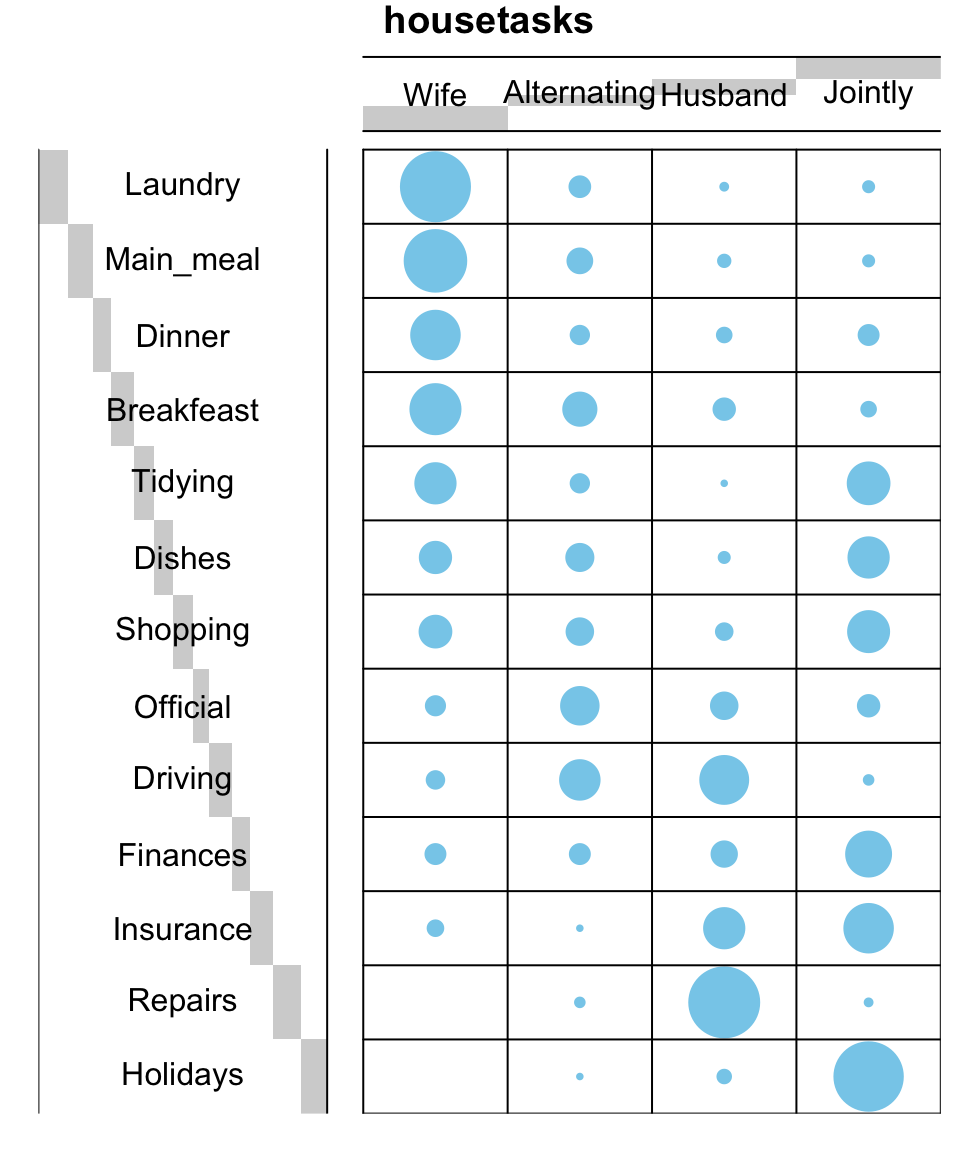
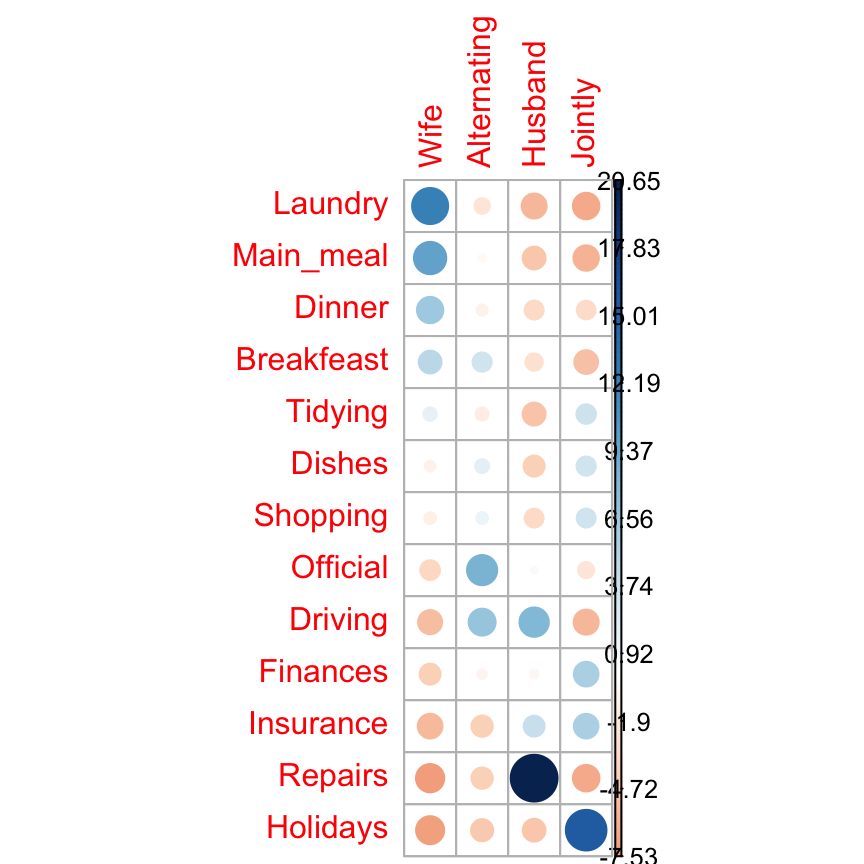
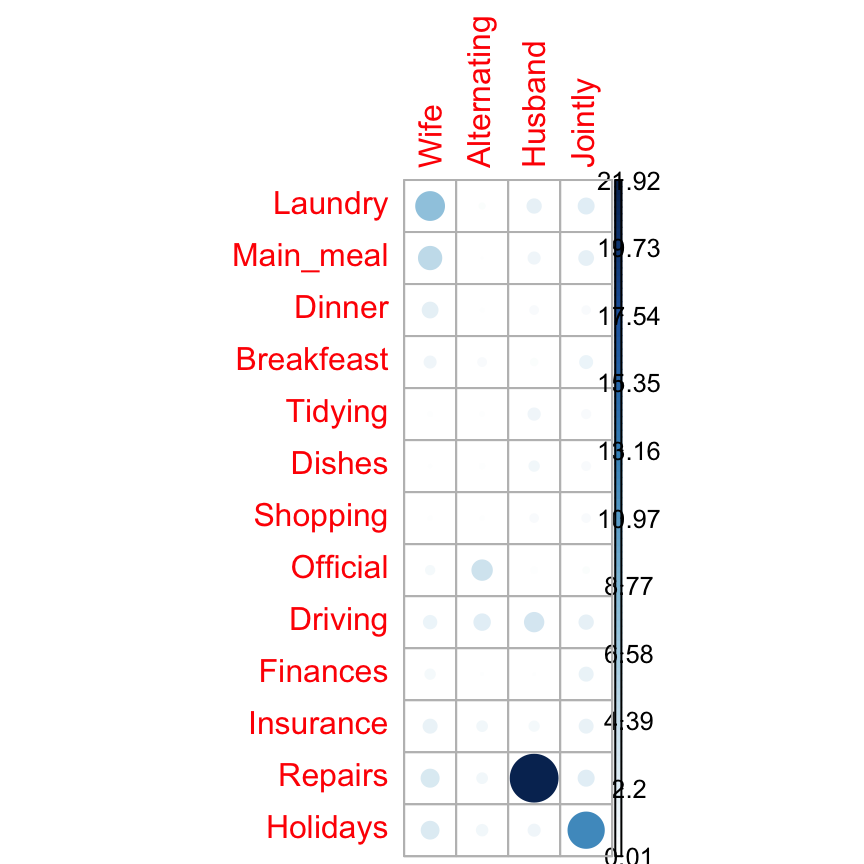
I’m very pleased to announce that survminer 0.3.0 is now available on CRAN. survminer makes it easy to create elegant and informative survival curves. It includes also functions for summarizing and inspecting graphically the Cox proportional hazards model assumptions.
This is a big release and a special thanks goes to Marcin Kosiński and Przemysław Biecek for their great works in actively improving and adding new features to the survminer package. The official online documentation is available at http://www.sthda.com/english/rpkgs/survminer/.
Release notes
In this post, we present only the most important changes in v0.3.0. See the release notes for a complete list.
New arguments in ggsurvplot()
data: Now, it’s recommended to specify the data used to compute survival curves (#142). This will avoid the error generated when trying to use the ggsurvplot() function inside another functions (@zzawadz, #125).
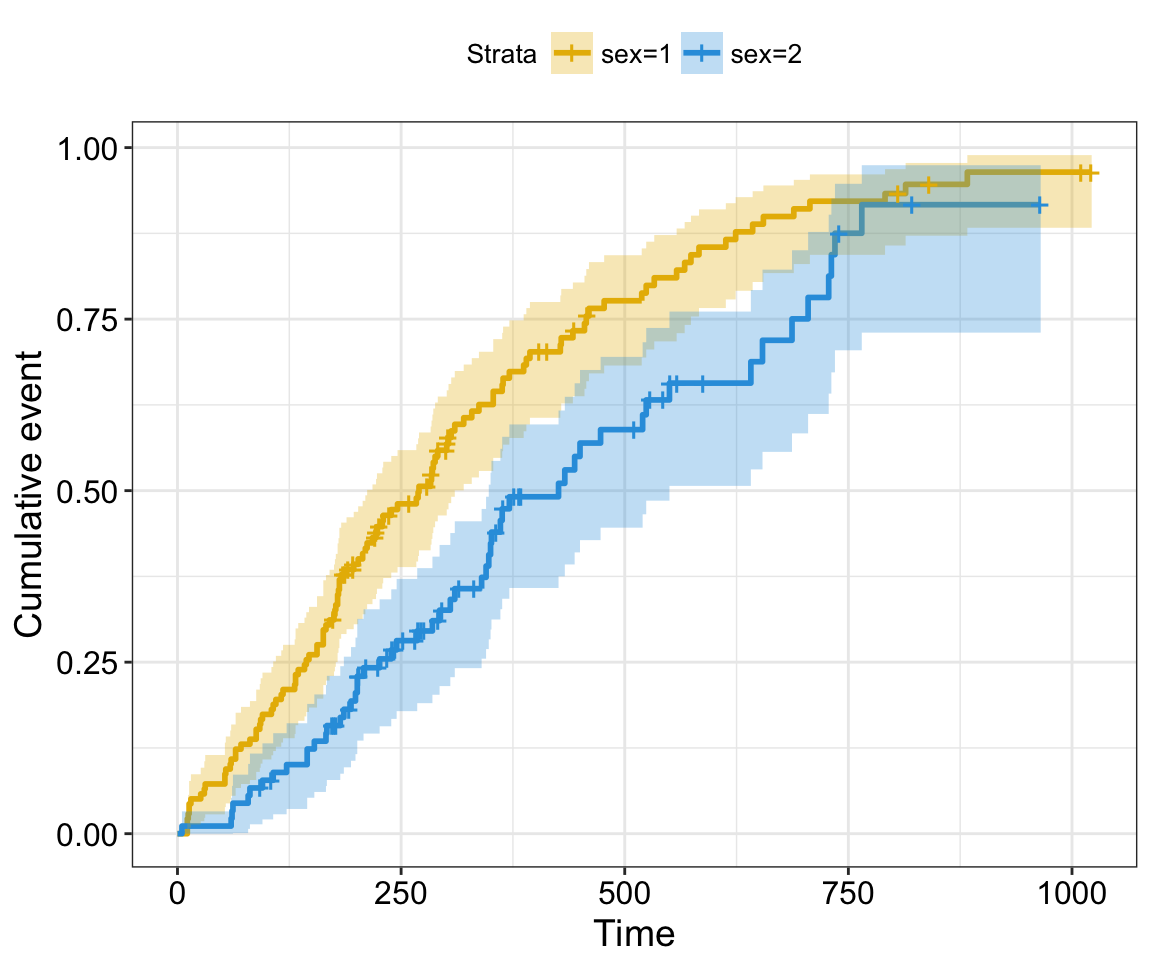
cumevents and cumcensor: logical value for displaying the cumulative number of events table (#117) and the cumulative number of censored subjects table (#155), respectively.
tables.theme for changing the theme of the tables under the main plot.
pval.method and log.rank.weights: New possibilities to compare survival curves. Functionality based on survMisc::comp (@MarcinKosinski, #17). Read also the following blog post on R-Addict website: Comparing (Fancy) Survival Curves with Weighted Log-rank Tests.
New functions
Thanks to the work of Przemysław Biecek, survminer 0.3.0 has received four new functions:
ggsurvevents() to plot the distribution of event’s times (@pbiecek, #116).
ggcoxadjustedcurves() to plot adjusted survival curves for Cox proportional hazards model (@pbiecek, #133&@markdanese, #67).
ggforest() to draw a forest plot (i.e. graphical summary) for the Cox model (@pbiecek, #114).
ggcompetingrisks() to plot the cumulative incidence curves for competing risks (@pbiecek, #168).
Vignettes and examples
Two new vignettes were contributed by Marcin Kosiński:
Installing and loading survminer
Install the latest developmental version from GitHub:
if(!require(devtools)) install.packages("devtools")
devtools::install_github("kassambara/survminer", build_vignettes = TRUE)
Or, install the latest release from CRAN as follow:
install.packages("survminer")
To load survminer in R, type this:
library("survminer")
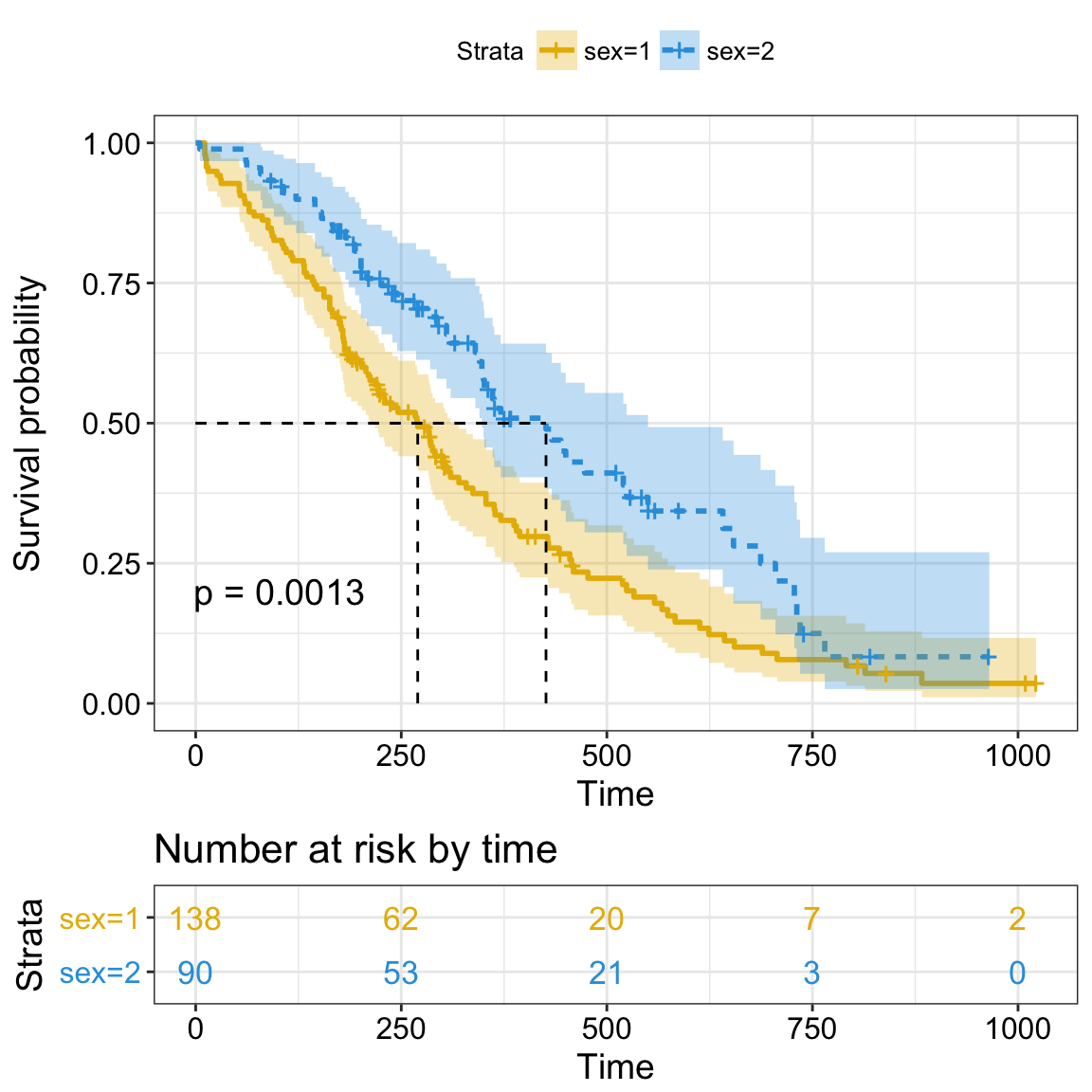
Survival curves
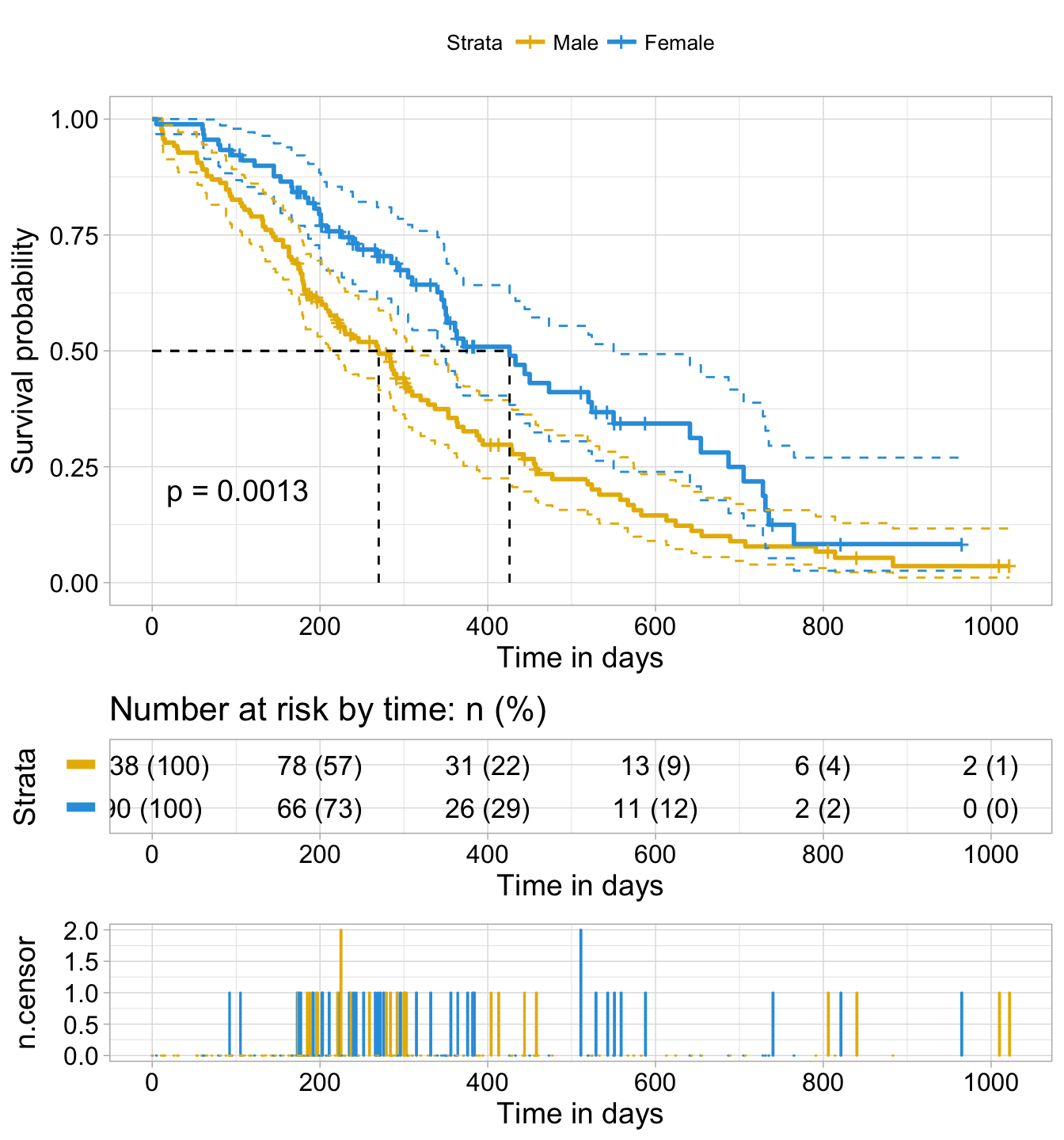
New arguments displaying supplementary survival tables - cumulative events & censored subjects - under the main survival curves:
- risk.table = TRUE: Displays the risk table
- cumevents = TRUE: Displays the cumulative number of events table.
- cumcensor = TRUE: Displays the cumulative number of censoring table.
- tables.height = 0.25: Numeric value (in [0 - 1]) to adjust the height of all tables under the main survival plot.
# Fit survival curves
require("survival")
fit <- survfit(Surv(time, status) ~ sex, data = lung)
# Plot informative survival curves
library("survminer")
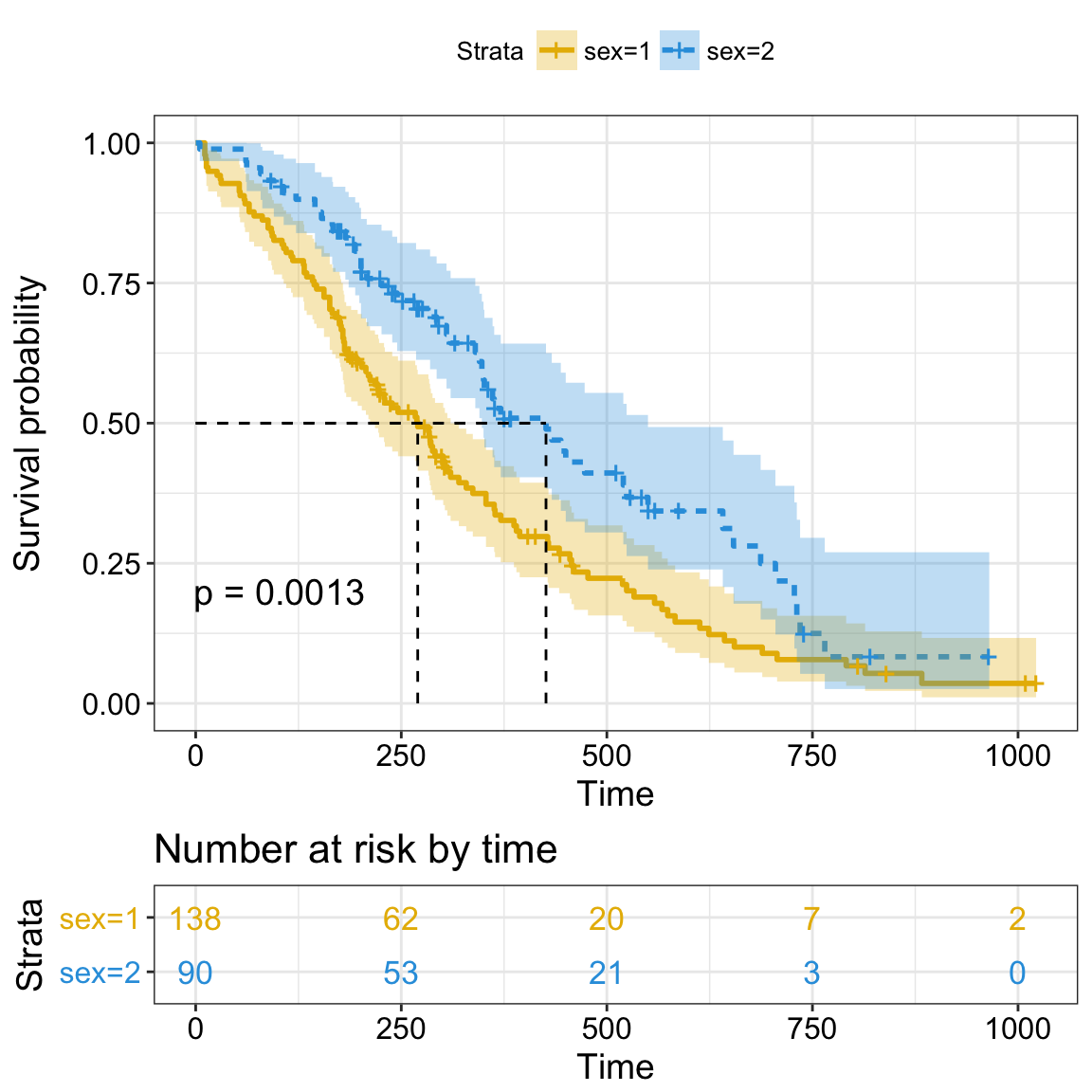
ggsurvplot(fit, data = lung,
title = "Survival Curves",
pval = TRUE, pval.method = TRUE, # Add p-value & method name
surv.median.line = "hv", # Add median survival lines
legend.title = "Sex", # Change legend titles
legend.labs = c("Male", "female"), # Change legend labels
palette = "jco", # Use JCO journal color palette
risk.table = TRUE, # Add No at risk table
cumevents = TRUE, # Add cumulative No of events table
tables.height = 0.15, # Specify tables height
tables.theme = theme_cleantable(), # Clean theme for tables
tables.y.text = FALSE # Hide tables y axis text
)
Cumulative events and censored tables are good additional feedback to survival curves, so that one could realize: what is the number of risk set AND what is the cause that the risk set become smaller: is it caused by events or by censored events?
Arranging multiple ggsurvplots on the same page
The function arrange_ggsurvplots() [in survminer] can be used to arrange multiple ggsurvplots on the same page.
# List of ggsurvplots
splots <- list()
splots[[1]] <- ggsurvplot(fit, data = lung,
risk.table = TRUE,
tables.y.text = FALSE,
ggtheme = theme_light())
splots[[2]] <- ggsurvplot(fit, data = lung,
risk.table = TRUE,
tables.y.text = FALSE,
ggtheme = theme_grey())
# Arrange multiple ggsurvplots and print the output
arrange_ggsurvplots(splots, print = TRUE,
ncol = 2, nrow = 1, risk.table.height = 0.25)
If you want to save the output into a pdf, type this:
# Arrange and save into pdf file
res <- arrange_ggsurvplots(splots, print = FALSE)
ggsave("myfile.pdf", res)
Distribution of events’ times
The function ggsurvevents() [in survminer] calculates and plots the distribution for events (both status = 0 and status = 1). It helps to notice when censoring is more common (@pbiecek, #116). This is an alternative to cumulative events and censored tables, described in the previous section.
For example in colon dataset, as illustrated below, censoring occur mostly after the 6’th year:
require("survival")
surv <- Surv(colon$time, colon$status)
ggsurvevents(surv)
Adjusted survival curves for Cox model
Adjusted survival curves show how a selected factor influences survival estimated from a cox model. If you want read more about why we need to adjust survival curves, see this document: Adjusted survival curves.
Briefly, in clinical investigations, there are many situations, where several known factors, potentially affect patient prognosis. For example, suppose two groups of patients are compared: those with and those without a specific genotype. If one of the groups also contains older individuals, any difference in survival may be attributable to genotype or age or indeed both. Hence, when investigating survival in relation to any one factor, it is often desirable to adjust for the impact of others.
The cox proportional-hazards model is one of the most important methods used for modelling survival analysis data.
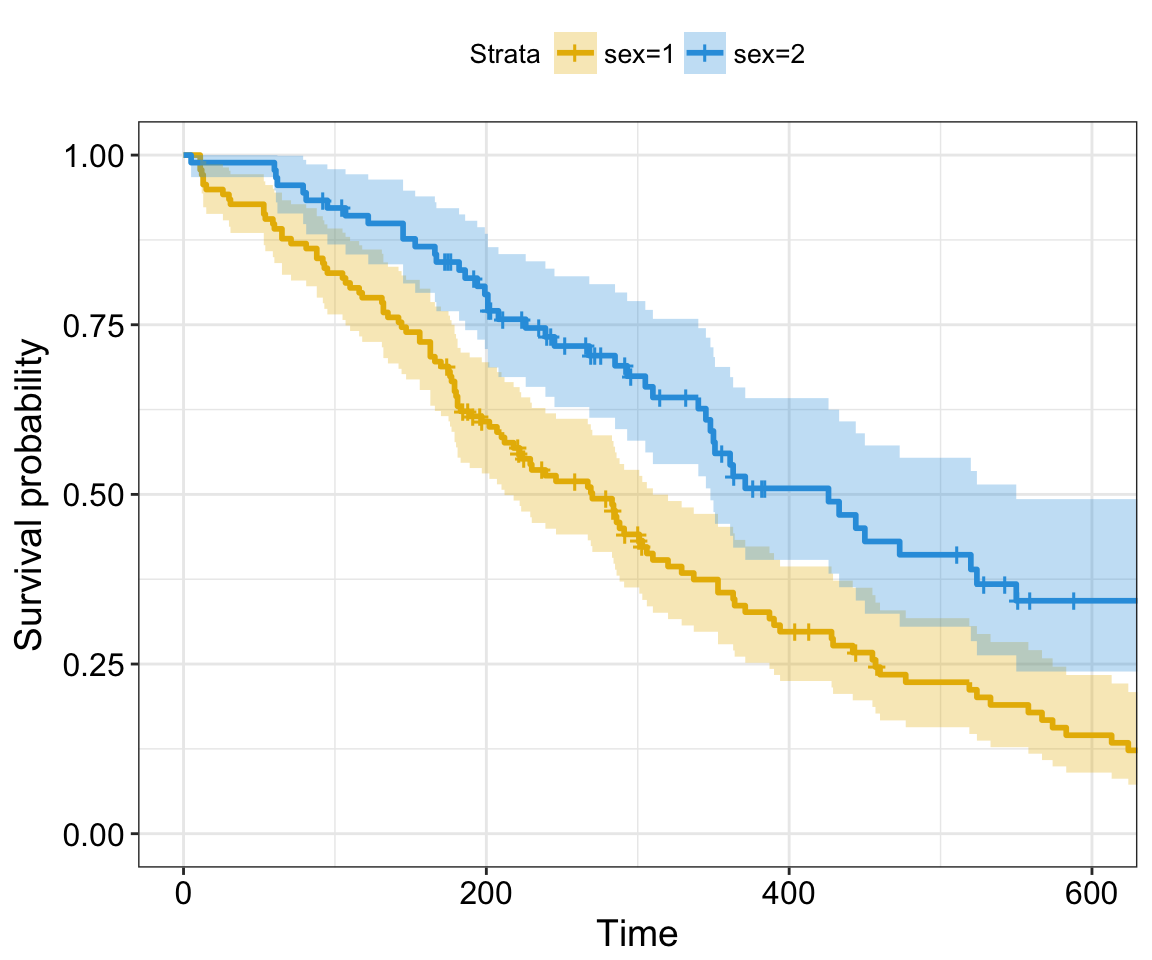
Here, we present the function ggcoxadjustedcurves() [in survminer] for plotting adjusted survival curves for cox proportional hazards model. The ggcoxadjustedcurves() function models the risks due to the confounders as described in the section 5.2 of this article: Terry M Therneau (2015); Adjusted survival curves. Briefly, the key idea is to predict survival for all individuals in the cohort, and then take the average of the predicted curves by groups of interest (for example, sex, age, genotype groups, etc.).
# Data preparation and computing cox model
library(survival)
lung$sex <- factor(lung$sex, levels = c(1,2),
labels = c("Male", "Female"))
res.cox <- coxph(Surv(time, status) ~ sex + age + ph.ecog, data = lung)
# Plot the baseline survival function
# with showing all individual predicted surv. curves
ggcoxadjustedcurves(res.cox, data = lung,
individual.curves = TRUE)
# Adjusted survival curves for the variable "sex"
ggcoxadjustedcurves(res.cox, data = lung,
variable = lung[, "sex"], # Variable of interest
legend.title = "Sex", # Change legend title
palette = "npg", # nature publishing group color palettes
curv.size = 2 # Change line size
)
Graphical summary of Cox model
The function ggforest() [in survminer] can be used to create a graphical summary of a Cox model, also known as forest plot. For each covariate, it displays the hazard ratio (HR) and the 95% confidence intervals of the HR. By default, covariates with significant p-value are highlighted in red.
# Fit a Cox model
library(survival)
res.cox <- coxph(Surv(time, status) ~ sex + age + ph.ecog, data = lung)
res.cox
## Call:
## coxph(formula = Surv(time, status) ~ sex + age + ph.ecog, data = lung)
##
## coef exp(coef) se(coef) z p
## sexFemale -0.55261 0.57544 0.16774 -3.29 0.00099
## age 0.01107 1.01113 0.00927 1.19 0.23242
## ph.ecog 0.46373 1.58999 0.11358 4.08 4.4e-05
##
## Likelihood ratio test=30.5 on 3 df, p=1.08e-06
## n= 227, number of events= 164
## (1 observation deleted due to missingness)
# Create a forest plot
ggforest(res.cox)
Pairwise comparisons for survival curves
When you compare three or more survival curves at once, the function survdiff() [in survival package] returns a global p-value whether to reject or not the null hypothesis.
With this, you know that a difference exists between groups, but you don’t know where. You can’t know until you test each combination.
Therefore, we implemented the function pairwise_survdiff() [in survminer]. It calculates pairwise comparisons between group levels with corrections for multiple testing.
- Multiple survival curves with global p-value:
library("survival")
library("survminer")
# Survival curves with global p-value
data(myeloma)
fit2 <- survfit(Surv(time, event) ~ molecular_group, data = myeloma)
ggsurvplot(fit2, data = myeloma,
legend.title = "Molecular Group",
legend.labs = levels(myeloma$molecular_group),
legend = "right",
pval = TRUE, palette = "lancet")
# Pairwise survdiff
res <- pairwise_survdiff(Surv(time, event) ~ molecular_group,
data = myeloma)
res
##
## Pairwise comparisons using Log-Rank test
##
## data: myeloma and molecular_group
##
## Cyclin D-1 Cyclin D-2 Hyperdiploid Low bone disease MAF MMSET
## Cyclin D-2 0.723 - - - - -
## Hyperdiploid 0.328 0.103 - - - -
## Low bone disease 0.644 0.447 0.723 - - -
## MAF 0.943 0.723 0.103 0.523 - -
## MMSET 0.103 0.038 0.527 0.485 0.038 -
## Proliferation 0.723 0.988 0.103 0.485 0.644 0.062
##
## P value adjustment method: BH
# Symbolic number coding
symnum(res$p.value, cutpoints = c(0, 0.0001, 0.001, 0.01, 0.05, 0.1, 1),
symbols = c("****", "***", "**", "*", "+", ""),
abbr.colnames = FALSE, na = "")
## Cyclin D-1 Cyclin D-2 Hyperdiploid Low bone disease MAF MMSET
## Cyclin D-2
## Hyperdiploid
## Low bone disease
## MAF
## MMSET * *
## Proliferation +
## attr(,"legend")
## [1] 0 '****' 1e-04 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1 \t ## NA: ''
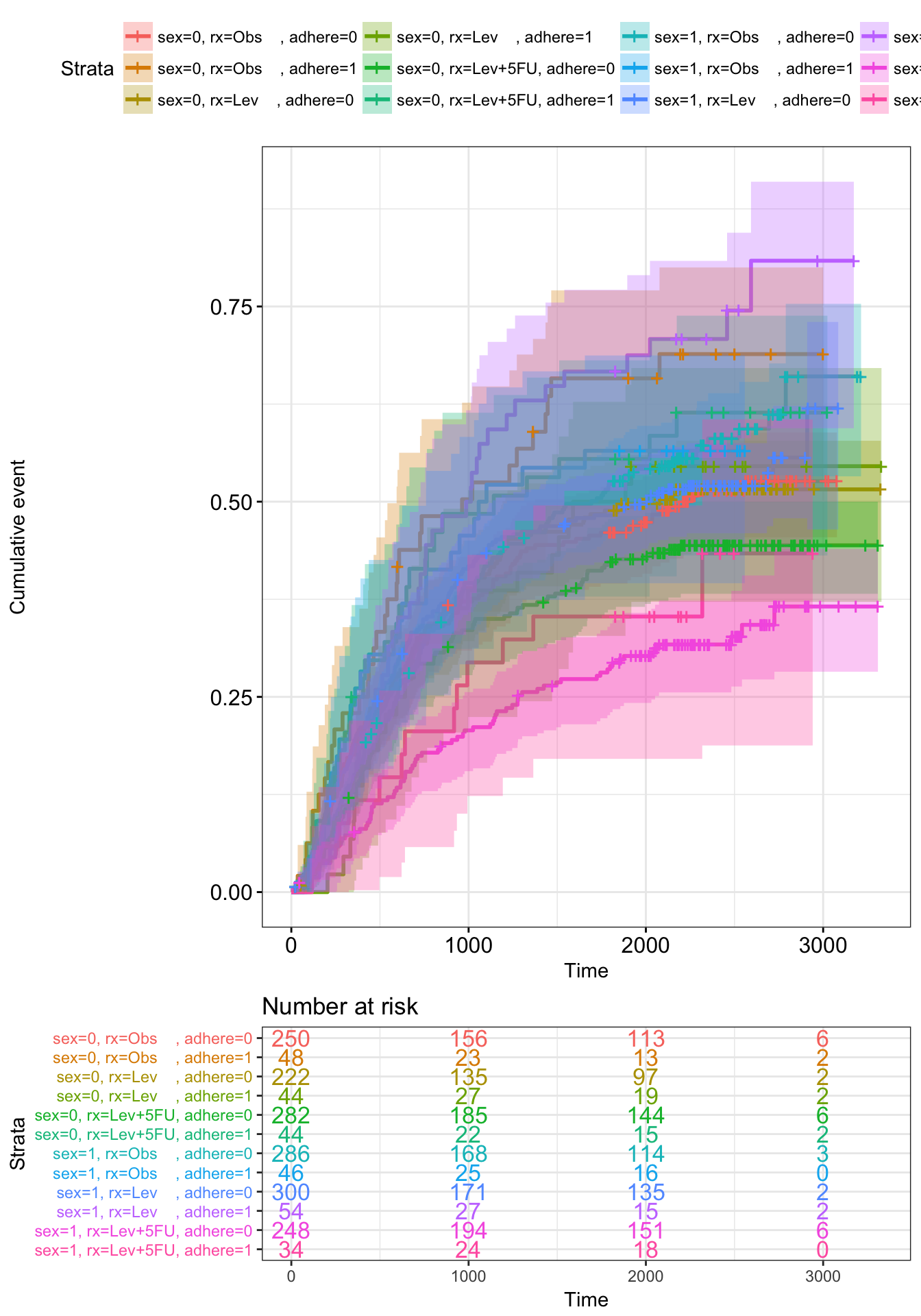
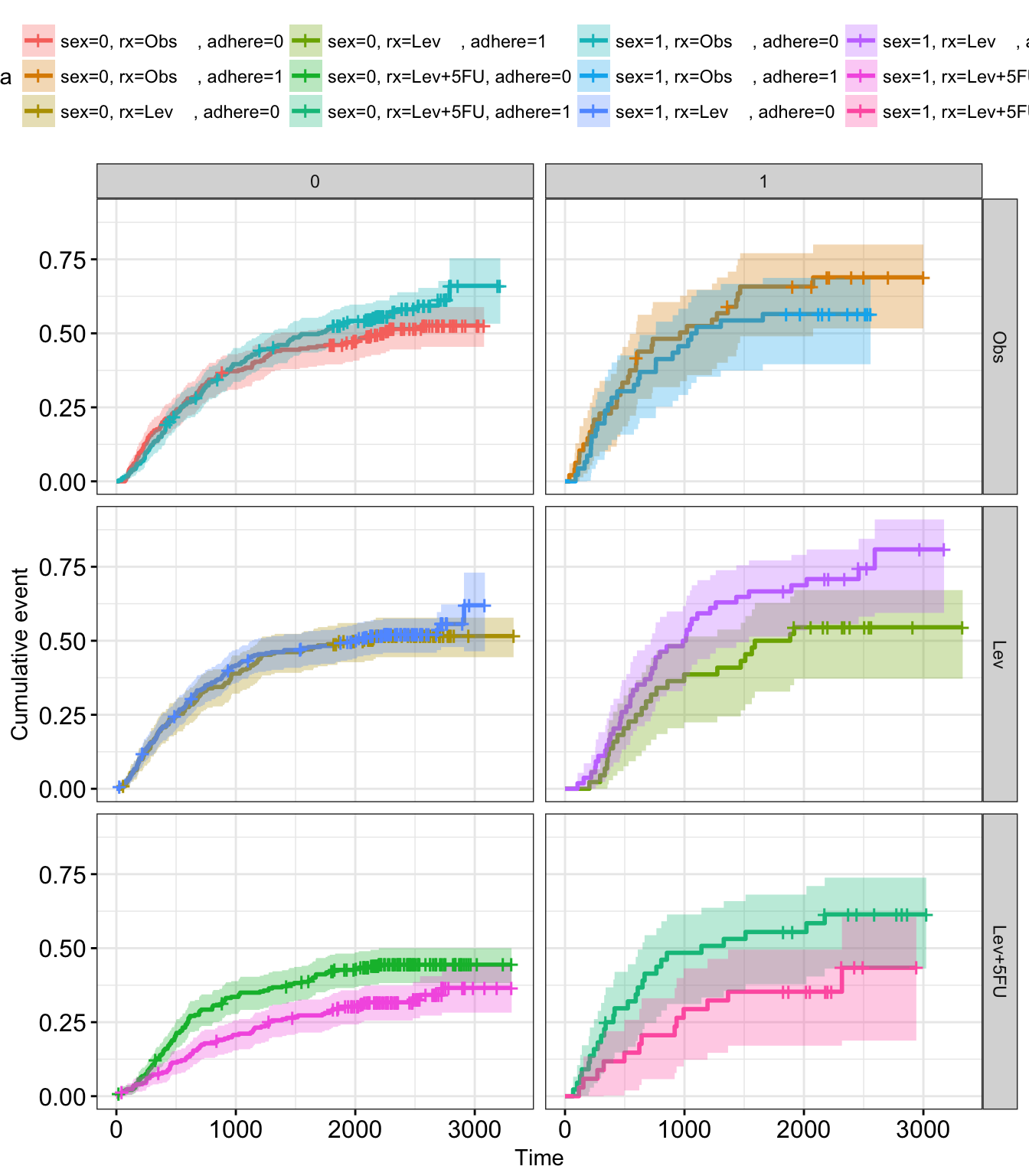
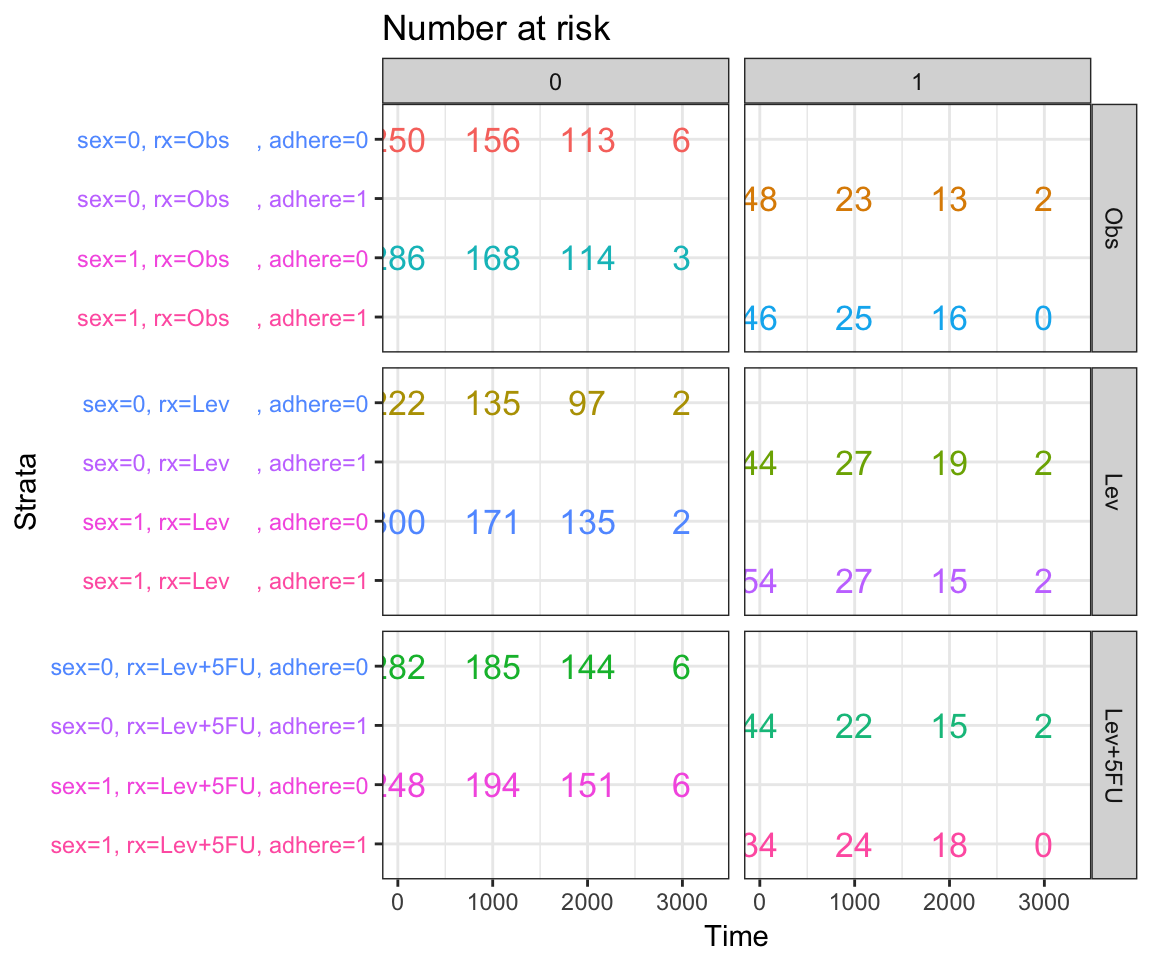
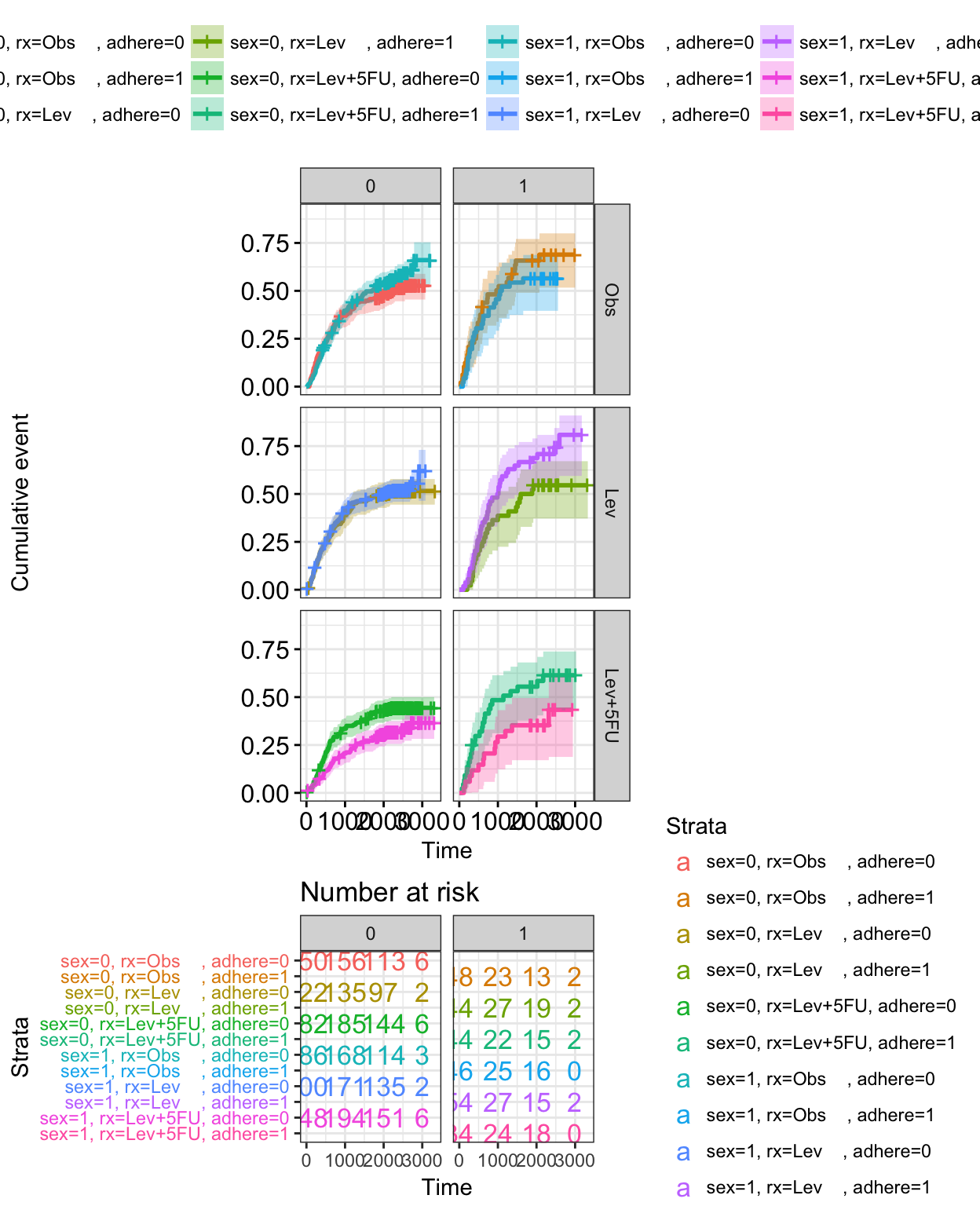
Visualizing competing risk analysis
Competing risk events refer to a situation where an individual (patient) is at risk of more than one mutually exclusive event, such as death from different causes, and the occurrence of one of these will prevent any other event from ever happening.
For example, when studying relapse in patients who underwent HSCT (Hematopoietic stem cell transplantation), transplant related mortality is a competing risk event and the cumulative incidence function (CIF) must be calculated by appropriate accounting.
A ‘competing risks’ analysis is implemented in the R package cmprsk. Here, we provide the ggcompetingrisks() function [in survminer] to plot the results using ggplot2-based elegant data visualization.
# Create a demo data set
#%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
set.seed(2)
failure_time <- rexp(100)
status <- factor(sample(0:2, 100, replace=TRUE), 0:2,
c('no event', 'death', 'progression'))
disease <- factor(sample(1:3, 100,replace=TRUE), 1:3,
c('BRCA','LUNG','OV'))
# Cumulative Incidence Function
#%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
require(cmprsk)
fit3 <- cuminc(ftime = failure_time, fstatus = status,
group = disease)
# Visualize
#%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
ggcompetingrisks(fit3, palette = "Dark2",
legend = "top",
ggtheme = theme_bw())
The ggcometingrisks() function has also support for multi-state survival objects (type = “mstate”), where the status variable can have multiple levels. The first of these will stand for censoring, and the others for various event types, e.g., causes of death.
# Data preparation
df <- data.frame(time = failure_time, status = status,
group = disease)
# Fit multi-state survival
library(survival)
fit5 <- survfit(Surv(time, status, type = "mstate") ~ group, data = df)
ggcompetingrisks(fit5, palette = "jco")
Infos
This analysis has been performed using R software (ver. 3.3.2).